Римские цифры
Ри́мские ци́фры — цифры, использовавшиеся древними римлянами в их непозиционной системе счисления.
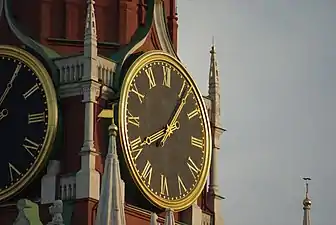
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская |
Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская |
Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая |
Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская |
Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
| Эта страница или раздел содержит специальные символы Unicode. Если у вас отсутствуют необходимые шрифты, некоторые символы могут отображаться неправильно. |
Натуральные числа записываются при помощи повторения этих цифр. При этом, если бо́льшая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая стоит перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.
Римские цифры появились за 500 лет до нашей эры у этрусков (см. этрусский алфавит), которые могли заимствовать часть цифр у прото-кельтов.
Римские цифры
Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Рим в VII веке до н. э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы.
Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Θ (или ⊕, или ⊗) и Φ (или ↀ , или CIƆ). Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения нет до сих пор. Согласно одной из распространённых теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещённые руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Θ и φ. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX ,а XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.
В целом римляне не были склонны заниматься математикой, поэтому не испытывали особой потребности в больших числах. Тем не менее для обозначения 10000 они эпизодически использовали символ CCIƆƆ , а для числа 100000 — символ CCCIƆƆƆ. Половинки этих символов иногда использовались для обозначения чисел 5000 (IƆƆ) и 50000 (IƆƆƆ).
Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова лат. uncia (унция), обозначавшего одну двенадцатую основной единицы длины[1][2].
| 1 | I | лат. unus, unum |
| 5 | V | лат. quinque |
| 10 | X | лат. decem |
| 50 | L | лат. quinquaginta |
| 100 | C | лат. centum |
| 500 | D | лат. quingenti |
| 1000 | M | лат. mille |
| Число | Обозначение |
|---|---|
| 1 | I |
| 2 | II |
| 3 | III |
| 4 | IV |
| 5 | V |
| 6 | VI |
| 7 | VII |
| 8 | VIII |
| 9 | IX |
| 10 | X |
| 11 | XI |
| 20 | XX |
| 30 | XXX |
| 40 | XL |
| 50 | L |
| 60 | LX |
| 70 | LXX |
| 80 | LXXX |
| 90 | XC |
| 100 | C |
| 200 | CC |
| 300 | CCC |
| 400 | CD |
| 500 | D; IƆ |
| 600 | DC; IƆC |
| 700 | DCC; IƆCC |
| 800 | DCCC; IƆCCC |
| 900 | CM; CCIƆ |
| 1000 | M; ↀ; CIƆ |
| 2000 | MM; CIƆCIƆ |
| 3000 | MMM; CIƆCIƆCIƆ |
| 3999 | MMMCMXCIX |
| 4000 | MV; ↀↁ; CIƆIƆƆ |
| 5000 | V; ↁ; IƆƆ |
| 6000 | VM; ↁↀ; IƆƆCIƆ |
| 7000 | VMM; ↁↀↀ; IƆƆCIƆCIƆ |
| 8000 | VMMM; ↁↀↀↀ; IƆƆCIƆCIƆCIƆ |
| 9000 | MX; ↀↂ; CIƆCCIƆƆ |
| 10 000 | X; ↂ; CCIƆƆ |
| 20 000 | XX; ↂↂ; CCIƆƆCCIƆƆ |
| 30 000 | XXX; ↂↂↂ; CCIƆƆCCIƆƆCCIƆƆ |
| 40 000 | XL; ↂↇ; CCIƆƆIƆƆƆ |
| 50 000 | L; ↇ; IƆƆƆ |
| 60 000 | LX; ↇↂ; IƆƆƆCCIƆƆ |
| 70 000 | LXX; ↇↂↂ; IƆƆƆCCIƆƆCCIƆƆ |
| 80 000 | LXXX; ↇↂↂↂ; IƆƆƆCCIƆƆCCIƆƆCCIƆƆ |
| 90 000 | XC; ↂↈ; CCIƆƆCCCIƆƆƆ |
| 100 000 | C; ↈ; CCCIƆƆƆ |
| 200 000 | CC; ↈↈ; CCCIƆƆƆCCCIƆƆƆ |
| 300 000 | CCC; ↈↈↈ; CCCIƆƆƆCCCIƆƆƆCCCIƆƆƆ |
| 400 000 | CD; CCCIƆƆƆIƆƆƆƆ |
| 500 000 | D; IƆƆƆƆ |
| 600 000 | DC; IƆƆƆƆCCCIƆƆƆ |
| 700 000 | DCC; IƆƆƆƆCCCIƆƆƆCCCIƆƆƆ |
| 800 000 | DCCC |
| 900 000 | CM |
| 1 000 000 | M |
| 2 000 000 | MM |
| 3 000 000 | MMM |
| 4 000 000 | MV |
| 5 000 000 | V |
| 6 000 000 | VM |
| 7 000 000 | VMM |
| 8 000 000 | VMMM |
| 9 000 000 | MX |
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
В системе римских цифр отсутствует ноль, но ранее использовалось обозначение нуля как nulla (нет), nihil (ничто) и N (первая буква этих слов).
При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трёх раз подряд; таким образом, с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX). В ранние периоды существовали знаки для обозначения бо́льших цифр — 5000, 10 000, 50 000 и 100 000 (тогда максимальное число по упомянутому правилу равно 399 999). При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается как CCLXXXIII, то есть 100+100+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза.
Пример: число 1988. Одна тысяча M, девять сотен CM, восемь десятков LXXX, восемь единиц VIII. Запишем их вместе: MCMLXXXVIII.
Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту: LXIV. Иногда черту рисовали и сверху, и снизу: XXXII — в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности). У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: V = 5000.

Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII». Существует и версия, что IV на циферблате не писалось потому, что IV — первые буквы имени бога Юпитера (IVPITER).
Меньшая цифра может быть записана и слева от большей, тогда её следует вычесть из большей. При этом вычитаться могут только цифры, обозначающие 1 или степени 10, а в качестве уменьшаемого выступать только ближайшие в числовом ряду к вычитаемой две цифры (то есть вычитаемое, умноженное на 5 или 10). Повторения меньшей цифры не допускаются. Таким образом, существует только шесть вариантов использования «правила вычитания»:
- IV = 4
- IX = 9
- XL = 40
- XC = 90
- CD = 400
- CM = 900
Например, число 94 будет XCIV = 100 − 10 + 5 − 1 = 94 — так называемое «правило вычитания» (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 — как XXXX).
Необходимо отметить, что другие способы «вычитания» недопустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел: например, в программе Microsoft Excel при преобразовании арабских цифр в римские при помощи функции «РИМСКОЕ()» можно использовать несколько видов представления чисел, от классического до сильно упрощённого (так, число 499 может быть записано как CDXCIX, LDVLIV, XDIX, VDIV или ID). Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:
- 999. Тысяча (M), вычтем 1 (I), получим 999 (IM) вместо CMXCIX. Следствие: 1999 — MIM вместо MCMXCIX
- 95. Сто (C), вычтем 5 (V), получим 95 (VC) вместо XCV
- 1950: Тысяча (M), вычтем 50 (L), получим 950 (LM). Следствие: 1950 — MLM вместо MCML
Случаи такой записи чисел (как правило, годов) часто встречаются в титрах телесериалов США. Например, для года 1998: MIIM вместо MCMXCVIII.
С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Например, число 123123 будет выглядеть так:
CXXIIICXXIII
А миллион как I, но только не с одной, а с двумя чертами во главе: I
Применение


В русском языке римские цифры используют в следующих случаях:
- Номер века или тысячелетия: XIX век, II тысячелетие до н. э.
- Спряжение глаголов.
- Маркировка циферблатов часов «под старину».
- Номер тома в многотомной книге или тома журналов (иногда — номера частей книги, разделов или глав).
- В музыкальной грамоте.
- Порядковый номер монарха.
- Группа крови на нашивках формы военнослужащих ВС РФ.
- На советских судах обозначали осадку в метрах римскими буквами (на английских кораблях — в футах римскими буквами).
- В некоторых изданиях — номера листов с предисловием к книге, чтобы не исправлять ссылки внутри основного текста при изменении предисловия.
- Иные важные события или пункты списка, например: V постулат Евклида, II мировая война, XX съезд КПСС, Игры XXII Олимпиады и тому подобное.
- Валентность химических элементов.
- Номер корпуса в вооружённых силах.
- Год окончания постройки здания на его фронтоне.
- Порядковый номер ступени в звукоряде.
- В математическом анализе римскими цифрами записывают номер производной, правда, при чтении (обычно) произносят «штрих» вместо I, «два штриха» вместо II, «три штриха» вместо III. Наконец, начиная с IV читают «четвёртая производная»: и .
Римские цифры широко употребляли в СССР при указании даты для обозначения месяца года, например: 11/III-85 или 9.XI.89, это можно увидеть на многих архивных документах тех времён. Подобным образом, через косую черту, в том числе записывали дату урока в классных журналах, например, 24/II. Для указания дат жизни и смерти на надгробиях часто использовали особый формат, где месяц года также обозначали римскими цифрами, например, (25 ноября 1887 ~ 26 января 1943). Подобный формат в 1970-1980-х годах использовали в медицинских справках.
С переходом на компьютерную обработку информации форматы даты, основанные на римских цифрах практически вышли из употребления.
В других языках сфера применения римских цифр может иметь особенности. В западных странах римскими цифрами нередко записывают номер года, например, на фронтонах зданий и в титрах видео-, кино- и телепродукции[3].
В современной Литве на дорожных знаках, на витринах магазинов, на вывесках предприятий римскими цифрами могут обозначать дни недели.
Юникод
Стандарт Юникода рекомендует использовать для представления римских цифр обычные латинские буквы[4]. Тем не менее стандарт включает также специальные символы для римских цифр как часть Числовых форм (англ. Number Forms)[5] в области знаков с кодами с U+2160 по U+2188. Например, MCMLXXXVIII может быть представлено в форме ⅯⅭⅯⅬⅩⅩⅩⅧ. Этот диапазон включает как строчные, так и прописные цифры для записи чисел от 1 (Ⅰ или I) до 12 (Ⅻ или XII), в том числе и комбинированные глифы для составных чисел, таких как 8 (Ⅷ или VIII), главным образом для обеспечения совместимости с восточноазиатскими наборами символов в таких промышленных стандартах, как JIS X 0213, где эти символы определены. Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ вместо его представления как Ⅹ и Ⅱ). В дополнение к этому, глифы существуют для архаичных[5] форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ), поздней формы записи 6 (ↅ, похожей на греческую стигму: Ϛ), ранней формы записи числа 50 (ↆ, похожей на стрелку, указывающую вниз ↓⫝⊥[6]), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ.
| Код | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение[7] | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 50 | 100 | 500 | 1 000 |
| U+2160 | Ⅰ 2160 |
Ⅱ 2161 |
Ⅲ 2162 |
Ⅳ 2163 |
Ⅴ 2164 |
Ⅵ 2165 |
Ⅶ 2166 |
Ⅷ 2167 |
Ⅸ 2168 |
Ⅹ 2169 |
Ⅺ 216A |
Ⅻ 216B |
Ⅼ 216C |
Ⅽ 216D |
Ⅾ 216E |
Ⅿ 216F |
| U+2170 | ⅰ 2170 |
ⅱ 2171 |
ⅲ 2172 |
ⅳ 2173 |
ⅴ 2174 |
ⅵ 2175 |
ⅶ 2176 |
ⅷ 2177 |
ⅸ 2178 |
ⅹ 2179 |
ⅺ 217A |
ⅻ 217B |
ⅼ 217C |
ⅽ 217D |
ⅾ 217E |
ⅿ 217F |
| Значение | 1 000 | 5 000 | 10 000 | 100 | 6 | 50 | 50 000 | 100 000 | ||||||||
| U+2180 | ↀ 2180 | ↁ 2181 | ↂ 2182 | Ↄ 2183 | ↅ 2185 | ↆ 2186 | ↇ 2187 | ↈ 2188 | ||||||||
Отображение всех этих символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы (например, шрифт Universalia).
Регулярные выражения
Регулярное выражение для проверки римских цифр — ^(M{0,3})(D?C{0,3}|C[DM])(L?X{0,3}|X[LC])(V?I{0,3}|I[VX])$[8]
В языке Perl для поиска римских цифр в строке можно использовать регулярное выражение
m/\b((?:M{0,3}?(?:D?C{0,3}|C[DM])?(?:L?X{0,3}|X[LC])?(?:I{0,3}?V?I{0,3}|I[VX])))\b/gs.
Преобразование
Для преобразования чисел, записанных арабскими цифрами в римские, используются специальные функции.
Например, в английской версии Microsoft Excel и в любой версии OpenOffice.org Calc для этого существует функция ROMAN (аргумент; форма), в русской версии Microsoft Excel эта функция называется РИМСКОЕ(число; форма). Необязательный аргумент «форма» может принимать значения от 0 до 4, а также «Ложь» и «Истина». Отсутствие аргумента «Форма» или равенство его 0 или «Истина» даёт «классическую» (строгую) форму преобразования; значение 4 или «Ложь» даёт наиболее упрощённую; значения 1, 2, 3 дают промежуточные по строгости-упрощению варианты. Различия проявляются, например, на числах 45, 49, 495, 499 (указаны первые в диапазоне [1;3999]).
| форма | 0 | 1 | 2 | 3 | 4 | |
| число | ||||||
| 45 | XLV | VL | VL | VL | VL | |
| 49 | XLIX | VLIV | IL | IL | IL | |
| 495 | CDXCV | LDVL | XDV | VD | VD | |
| 499 | CDXCIX | LDVLIV | XDIX | VDIV | ID |
Для нецелых значений аргумента «число» производится округление вниз до целого; если после этого значение оказывается больше 3999 или меньше 0, то функция возвращает «#Знач»; для значения 0 возвращается пустая ячейка.
var arab = [1, 4, 5, 9, 10, 40, 50, 90, 100, 400, 500, 900, 1000];
var roman = ['I','IV','V','IX','X','XL','L','XC','C','CD','D','CM','M'];
function arabToRoman(number)
{
if(!number) return '';
var ret = '';
var i = arab.length - 1;
while(number > 0)
{
if(number >= arab[i])
{
ret += roman[i];
number -= arab[i];
}
else
{
i--;
}
}
return ret;
}
function romanToArab(str)
{
str = str.toUpperCase();
var ret = 0;
var i = arab.length - 1;
var pos = 0;
while(i >= 0 && pos < str.length )
{
if(str.substr(pos, roman[i].length) == roman[i])
{
ret += arab[i];
pos += roman[i].length;
}
else
{
i--;
}
}
return ret;
}
#include <string.h>
const int arabar[] = { 1, 4, 5, 9, 10, 40, 50, 90, 100, 400, 500, 900, 1000};
const char *romanar[] = { "I", "IV", "V", "IX", "X", "XL", "L", "XC", "C", "CD", "D", "CM", "M"};
char *arab2roman(unsigned short int arab) {
static char roman[80];
const int m = sizeof(arabar)/sizeof(int)-1, arabmax=arabar[m];
const char romanmax=romanar[m][0];
int i, n;
if(!arab) {
*roman=0;
return roman;
}
i=0;
while(arab>arabmax) {
roman[i++] = romanmax;
arab -= arabmax;
}
n=m;
while(arab > 0) {
if(arab >= arabar[n]) {
roman[i++] = romanar[n][0];
if(n&1)
roman[i++] = romanar[n][1];
arab -= arabar[n];
} else
n--;
}
roman[i]=0;
return roman;
}
unsigned short int roman2arab(char *roman) {
const int m = sizeof(arabar)/sizeof(int)-1;
unsigned short int arab;
int len, n, i, pir;
len=strlen(roman);
arab=0;
n=m;
i=0;
while(n >= 0 && i < len) {
pir=n&1;
if(roman[i] == romanar[n][0] && (!pir || roman[i+1] == romanar[n][1])) {
arab += arabar[n];
i += 1+pir;
} else
n--;
}
return arab;
}
val arabar = Array(1, 4, 5, 9, 10, 40, 50, 90, 100, 400, 500, 900, 1000)
val romanar = Array("I", "IV", "V", "IX", "X", "XL", "L", "XC", "C", "CD", "D", "CM", "M")
def arab2roman(arab: Int, acc: String = "", n: Int = arabar.length - 1): String =
if (arab == 0) acc
else if (arab >= arabar(n)) arab2roman(arab - arabar(n), acc + romanar(n), n)
else arab2roman(arab, acc, n-1)
// arab2roman(4933) = MMMMCMXXXIII
type str2 = string[2];
const
Rims : array[1..14] of str2 = ('M','CM','D','CD','C','XC','L','XL','X','IX','V','IV','I',' ');
Arab : array[1..14] of integer = (1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1, 0);
var
N, NI, I, J : integer;
S : string;
function Arab2Rim(N : integer) : string;
var S : string;
I : integer;
begin
S := ''; I:=1;
while N > 0 do begin
while Arab[I]<=N do begin
S := S + Rims[I];
N := N - Arab[I]
end;
I:=I+1
end;
Arab2Rim := S
end;
function Rim2Arab (S:string) : integer;
var I, N : integer;
begin
I:=1; N := 0;
while S<>'' do begin
while Rims[I] = Copy(S, 1, Length(Rims[I]) ) do begin
S := Copy( S, 1+Length(Rims[I]), 255);
N := N + Arab[I]
end;
I:=I+1
end;
Rim2Arab := N
end;
begin
WriteLn('Перевод из арабских цифр в римские. 1999 B_SA');
{ Write('Введите число для преобразования:'); ReadLn(N);}
for NI := 26 to 46 do
WriteLn(NI,' = ',Arab2Rim(NI),' обратно ', Rim2Arab( Arab2Rim(NI) ));
end.
function Arab2Roman(arab:integer):string;
var
i:integer;
d:integer;
arab_str:string;
arab_len:integer;
begin
Result := '';
arab_str := IntToStr(arab);
arab_len := Length(arab_str);
for i := 0 to arab_len-1 do begin
d := StrToInt(String(arab_str[arab_len-i]));
if (d+1) mod 5 = 0 then
Result := Copy('IXCM', 1+i, 1) + Copy('VXLCDM', i*2 + (d+1) div 5, 1) + Result
else
Result := Copy('VLD', 1+i, d div 5) + Copy('IIIXXXCCCMMM', 1+i*3, (d mod 5)) + Result;
end;
end;
10 INPUT "АРАБСКОЕ ЧИСЛО: "; А$
20 FOR I=0 TO LEN(A$)-1
30 X=VAL(MID$(A$,LEN(A$)-I,1))
40 IF X=4 OR X=9 THEN B$=MID$("IXCM",I+1,1)+MID$("VXLCDM",I*2+(X+1)/5,1)+B$
50 IF X<4 THEN B$=MID$("IIIXXXCCCMMM",1+I*3,X)+B$
ELSE IF X>4 AND X<9 THEN B$=MID$("VLD",I+1,1)+MID$("IIIXXXCCCMMM",1+I*3,X-5)+B$
60 NEXT I
70 PRINT "РИМСКОЕ ЧИСЛО: "; B$
string-join(
for $num in (1999)
return (
('','M','MM','MMM')[($num idiv 1000) mod 10+1],
('','C','CC','CCC','CD','D','DC','DCC','DCCC','CM')[($num idiv 100) mod 10+1],
('','X','XX','XXX','XL','L','LX','LXX','LXXX','XC')[($num idiv 10) mod 10+1],
('','I','II','III','IV','V','VI','VII','VIII','IX')[$num mod 10+1]
),
'')
use strict;
use warnings;
my $n = 1999;
my $nums = [
['', qw(I II III IV V VI VII VIII IX) ],
['', qw(X XX XXX XL L LX LXX LXXX XC) ],
['', qw(C CC CCC CD D DC DCC DCCC CM) ],
['', qw(M MM MMM) ]
];
my $i = 0; my @res = ();
push @res, ($nums->[$i++][ ($n % 10, $n = int($n / 10))[0] ]) for 0 .. 3;
print reverse @res;
import java.util.*;
public class IntegerConverter {
public static String intToRoman(int number) {
if (number >= 4000 || number <= 0)
return null;
StringBuilder result = new StringBuilder();
for(Integer key : units.descendingKeySet()) {
while (number >= key) {
number -= key;
result.append(units.get(key));
}
}
return result.toString();
}
private static final NavigableMap<Integer, String> units;
static {
NavigableMap<Integer, String> initMap = new TreeMap<>();
initMap.put(1000, "M");
initMap.put(900, "CM");
initMap.put(500, "D");
initMap.put(400, "CD");
initMap.put(100, "C");
initMap.put(90, "XC");
initMap.put(50, "L");
initMap.put(40, "XL");
initMap.put(10, "X");
initMap.put(9, "IX");
initMap.put(5, "V");
initMap.put(4, "IV");
initMap.put(1, "I");
units = Collections.unmodifiableNavigableMap(initMap);
}
}
/// <summary>
/// Класс предназначен для преобразований арабских чисел в римские и обратно
/// </summary>
/// <remarks>
/// <para>Класс изначально содержит алфавит римских чисел, способных определять арабские числа от 1 до 39999</para>
/// <para>Если необходимо расширить диапазон, то можно определить дополнительные обозначения для римских чисел, используя
/// поле <see cref="БазовыеРимскиеЧисла"/>БазовыеРимскиеЧисла</remarks>
public static class РимскоеЧисло
{
/// <summary>
/// Алфавит базовых римских чисел
/// <para>Алфавит построен в виде словаря. Ключом словаря является арабское число (int), значением - соответствующее ему
/// римское число (string)</para>
/// </summary>
/// <remarks>
/// <para>Содержит римское обозначения арабских чисел 1*,4*,5*,9* - где "*"представляет собой 0...N нулей</para>
/// <para>При создании содержит в себе обозначение чисел от 1 до 10000 (I...ↂ) Так как в римском числе один символ не может
/// встречаться более трех раз, то изначально можно преобразовать в римский формат числа от 1 до 39999.</para>
/// <para>Если Вы хотите иметь возможность работать с большим количеством римских чисел, то вы должны добавить в список
/// дополнительные обозначения начиная с 40000 не пропуская элементы 1*,4*,5*,9*.</para>
/// </remarks>
public static SortedList<int, string> БазовыеРимскиеЧисла { get; set; }
static РимскоеЧисло()
{
БазовыеРимскиеЧисла = new SortedList<int, string>(17);
БазовыеРимскиеЧисла.Add(1, "I");
БазовыеРимскиеЧисла.Add(4, "IV");
БазовыеРимскиеЧисла.Add(5, "V");
БазовыеРимскиеЧисла.Add(9, "IX");
БазовыеРимскиеЧисла.Add(10, "X");
БазовыеРимскиеЧисла.Add(40, "XL");
БазовыеРимскиеЧисла.Add(50, "L");
БазовыеРимскиеЧисла.Add(90, "XC");
БазовыеРимскиеЧисла.Add(100, "C");
БазовыеРимскиеЧисла.Add(400, "CD");
БазовыеРимскиеЧисла.Add(500, "D");
БазовыеРимскиеЧисла.Add(900, "CM");
БазовыеРимскиеЧисла.Add(1000, "M");
БазовыеРимскиеЧисла.Add(4000, "Mↁ");
БазовыеРимскиеЧисла.Add(5000, "ↁ");
БазовыеРимскиеЧисла.Add(9000, "Mↂ");
БазовыеРимскиеЧисла.Add(10000, "ↂ");
}
/// <summary>
/// Рассчитывает максимально возможное римское число для текущего алфавита римских чисел.
/// </summary>
/// <returns>Максимально возможное римское число</returns>
public static uint МаксимальноеРимскоеЧисло()
{
int последнееЧисло = БазовыеРимскиеЧисла.Keys.Last();
int числоБезНулей = int.Parse(последнееЧисло.ToString().Replace('0','\0'));
int предварительное=0;
switch (числоБезНулей)
{
case 1:
предварительное = последнееЧисло * 4 - 1;
break;
case 4:
case 9:
предварительное = последнееЧисло;
break;
case 5:
предварительное = последнееЧисло + последнееЧисло / 5 * 3;
break;
default:
break;
}
return uint.Parse(предварительное.ToString().Replace('0', '9'));;
}
/// <summary>
/// Конвентирует целое число в римское число
/// </summary>
/// <param name="числоАраб">Арабское число, которое необходимо преобразовать в римскую запись</param>
/// <exception cref="ArgumentOutOfRangeException">Генерируется когда в качестве параметра передано число равное "0"
/// или число большее чем максимальная римское число.</exception>
/// <returns>Строку, представляющую собой римской число</returns>
public static string АрабскоеВРимское(this int числоАраб)
{
StringBuilder числоРимское = new StringBuilder();
//Исключаем знак "-" из арабского числа и делаем его первым символом римского числа
if (числоАраб < 0)
{
числоРимское.Append("-");
числоАраб = -числоАраб;
}
if (числоАраб == 0)
throw new ArgumentOutOfRangeException("числоАраб", числоАраб,
"Недопустимое значение аргумента: римские числа не могут быть равными\"0\"");
else if (числоАраб > МаксимальноеРимскоеЧисло())
throw new ArgumentOutOfRangeException("числоАраб", числоАраб,
string.Format("Недопустимое значение аргумента: невозможно задать римское число большее чем {0}",
МаксимальноеРимскоеЧисло()));
//Раскладываем арабское число на составляющие его римские числа и объединяем их в одну строку
var необходимыеБазовыеРимскиеЧисла =
from к in БазовыеРимскиеЧисла.Keys
where к <= числоАраб
orderby к descending
select к;
foreach (int тек in необходимыеБазовыеРимскиеЧисла)
{
while ((числоАраб / тек) >= 1)
{
числоАраб -= тек;
числоРимское.Append(БазовыеРимскиеЧисла[тек]);
}
}
return числоРимское.ToString();
}
/// <summary>
/// Конвентирует римское число в арабское
/// </summary>
/// <param name="числоРимское">Римское число, которое необходимо преобразовать в тип int</param>
/// <exception cref="FormatException">Генерируется когда в качестве параметра передано число не являющееся римским</exception>
/// <returns>Целое число, представляющее собой арабскую запись римского числа</returns>
public static int РимскоеВАрабское(this string числоРимское)
{
int числоАраб = 0;
sbyte отрицательное = 1;
string рим = числоРимское.Trim();
if (рим[0] == '-')
{
отрицательное = -1;
рим = рим.Substring(1);
}
StringBuilder шаблонРимскогоНомера = new StringBuilder();
foreach (int к in БазовыеРимскиеЧисла.Keys)
{
int индекс = БазовыеРимскиеЧисла.Keys.IndexOf(к);
string квантификатор="?";
if (индекс == 0 || (индекс % 4) == 0)
квантификатор="{0,3}";
шаблонРимскогоНомера.Insert(0, string.Format("(?<{0}>({1}){2})?", к.ToString(),
БазовыеРимскиеЧисла[к], квантификатор));
}
//Игнорировать регистр + соответствие должно начинаться с начала строки
шаблонРимскогоНомера.Insert(0, "(?i)^");
//Соответствие должно обнаруживаться в конце строки
шаблонРимскогоНомера.Append("$");
//Упрощенная проверка. Не проверяет таких ошибок как IVII
if (!Regex.IsMatch(рим, шаблонРимскогоНомера.ToString()))
throw new FormatException(string.Format("Текст \"{0}\" не является римским числом",числоРимское));
Match число = Regex.Match(рим, шаблонРимскогоНомера.ToString());
foreach (int к in БазовыеРимскиеЧисла.Keys)
{
числоАраб += число.Groups[к.ToString()].Length / БазовыеРимскиеЧисла[к].Length * к;
}
return числоАраб * отрицательное;
}
}
Примечания
- Цифры и системы счисления. Онлайн Энциклопедия Кругосвет.
- М. Я. Выгодский «Справочник по элементарной математике» Москва 1958 г. Государственное издательство физико-математической литературы. стр.62
- Beckham’s road to Roman // Би-би-си, 17 April, 2002
- Unicode Standard, 15.3 («For most purposes, it is preferable to compose the Roman numerals from sequences of the appropriate Latin letters.»)
- Unicode Number Forms
- Perry, David J. Proposal to Add Additional Ancient Roman Characters to UCS.
- Для первых двух строк
- Глава 31. Римская числовая нотация :: Идеи реализации
- "Наука и жизнь" N12 1986 стр.95, В.Птицын, г.Москва
- Автор - Кузнецов Евгений А.
- Автор - Кузнецов Евгений А., 1992 год
