Постоянная Апери

Двухпетлевая диаграмма Фейнмана, результат для которой содержит ${\displaystyle \zeta (3)}$

В математике постоянная Апери встречается во многих приложениях. В частности, величина, обратная ${\displaystyle \zeta (3)}$, даёт вероятность того, что любые три случайным образом выбранных положительных целых числа будут взаимно просты — в том смысле, что при ${\displaystyle N\to \infty }$ вероятность того, что три положительных целых числа, меньших, чем ${\displaystyle {\textstyle {N}}}$ (и выбранных случайным образом) будут взаимно простыми, стремится к ${\displaystyle 1/\zeta (3)}$.

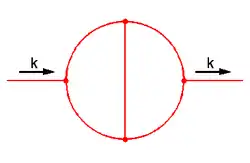
Постоянная Апери естественным образом возникает в ряде проблем физики, включая поправки второго (и выше) порядков к аномальному магнитному моменту электрона в квантовой электродинамике. Например, результат для двухпетлевой диаграммы Фейнмана, изображённой на рисунке, даёт ${\displaystyle 6\zeta (3)}$ (здесь предполагается 4-мерное интегрирование по импульсам внутренних петель, содержащих только безмассовые виртуальные частицы, а также соответствующая нормировка, включая степень импульса внешней частицы ${\displaystyle k}$). Другой пример — двумерная модель Дебая.

Постоянная Апери связана с частным значением полигамма-функции второго порядка:

${\displaystyle \zeta (3)=-{\tfrac {1}{2}}\,\psi ^{(2)}(1)}$

и появляется в разложении гамма-функции в ряд Тейлора:

${\displaystyle \Gamma (1+\varepsilon )=e^{-\gamma \varepsilon }\left[1+{\tfrac {1}{12}}\pi ^{2}\varepsilon ^{2}-{\tfrac {1}{3}}\zeta (3)\varepsilon ^{3}+O(\varepsilon ^{4})\right]}$,

где в виде ${\displaystyle e^{-\gamma \varepsilon }}$ факторизуются вклады, содержащие постоянную Эйлера — Маскерони ${\displaystyle {\textstyle {\gamma }}}$.

Постоянная Апери также связана со значениями трилогарифма ${\displaystyle \mathrm {Li} _{3}(z)}$ (частный случай полилогарифма ${\displaystyle \mathrm {Li} _{n}(z)}$):

${\displaystyle \mathrm {Li} _{3}(1)=\zeta (3)}$,

${\displaystyle \mathrm {Li} _{3}\left({\tfrac {1}{2}}\right)={\tfrac {1}{6}}(\ln 2)^{3}-{\tfrac {1}{12}}\pi ^{2}\ln 2+{\tfrac {7}{8}}\,\zeta (3)}$.

Некоторые другие ряды, члены которых обратны к кубам натуральных чисел, также выражаются через постоянную Апери:

${\displaystyle \zeta (3)={\tfrac {4}{3}}\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{k^{3}}}={\tfrac {4}{3}}\left(1-{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}-{\frac {1}{4^{3}}}+\cdots \right)}$,

${\displaystyle \zeta (3)={\tfrac {8}{7}}\sum _{k=0}^{\infty }{\frac {1}{(2k+1)^{3}}}={\tfrac {8}{7}}\left(1+{\frac {1}{3^{3}}}+{\frac {1}{5^{3}}}+{\frac {1}{7^{3}}}+\cdots \right)}$.

Другие известные результаты — сумма ряда, содержащего гармонические числа ${\displaystyle {\textstyle {H_{k}}}}$:

${\displaystyle \zeta (3)={\tfrac {1}{2}}\sum _{k=1}^{\infty }{\frac {H_{k}}{k^{2}}}}$,

а также двукратная сумма:

${\displaystyle \zeta (3)={\tfrac {1}{2}}\sum _{j=1}^{\infty }\sum _{k=1}^{\infty }{\frac {1}{jk(j+k)}}}$.

Для доказательства иррациональности ${\displaystyle \zeta (3)}$ Роже Апери[3] пользовался представлением:

${\displaystyle \zeta (3)={\tfrac {5}{2}}\sum _{k=1}^{\infty }(-1)^{k-1}{\frac {(k!)^{2}}{k^{3}(2k)!}}={\tfrac {5}{2}}\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{k^{3}{\binom {2k}{k}}}}}$,

где ${\displaystyle {\textstyle {\binom {2k}{k}}={\frac {(2k)!}{k!^{2}}}}}$ — биномиальный коэффициент.

В 1773 году Леонард Эйлер[7] привёл представление в виде ряда[8] (которое впоследствии было несколько раз заново открыто в других работах):

${\displaystyle \zeta (3)={\tfrac {1}{7}}\pi ^{2}\left[1-4\sum _{k=1}^{\infty }{\frac {\zeta (2k)}{(2k+1)(2k+2)2^{2k}}}\right]}$,

в котором значения дзета-функции Римана чётных аргументов могут быть представлены как ${\displaystyle {\textstyle {\zeta (2k)=(-1)^{k+1}(2\pi )^{2k}B_{2k}/(2(2k)!)}}}$, где ${\displaystyle {\textstyle {B_{2k}}}}$ — числа Бернулли.

Рамануджан дал несколько представлений в виде рядов, которые замечательны тем, что они обеспечивают несколько новых значащих цифр на каждой итерации. Они включают в себя[9]:

${\displaystyle \zeta (3)={\tfrac {7}{180}}\pi ^{3}-2\sum _{k=1}^{\infty }{\frac {1}{k^{3}(e^{2\pi k}-1)}}}$

Саймон Плафф получил ряды другого типа[10]

${\displaystyle \zeta (3)=14\sum _{k=1}^{\infty }{\frac {1}{k^{3}\sinh(\pi k)}}-{\tfrac {11}{2}}\sum _{k=1}^{\infty }{\frac {1}{k^{3}(e^{2\pi k}-1)}}-{\tfrac {7}{2}}\sum _{k=1}^{\infty }{\frac {1}{k^{3}(e^{2\pi k}+1)}}\;,}$

а также аналогичные представления для других постоянных ${\displaystyle \zeta (2n+1)}$.

Были также получены другие представления в виде рядов, включая:

${\displaystyle \zeta (3)={\tfrac {1}{4}}\sum _{k=1}^{\infty }(-1)^{k-1}{\frac {(56k^{2}-32k+5)(k-1)!^{3}}{(2k-1)^{2}(3k)!}}}$

${\displaystyle \zeta (3)={\tfrac {8}{7}}-{\tfrac {8}{7}}\sum _{k=1}^{\infty }{\frac {{\left(-1\right)}^{k}\,2^{-5+12\,k}\,k\,\left(-3+9\,k+148\,k^{2}-432\,k^{3}-2688\,k^{4}+7168\,k^{5}\right)\,{k!}^{3}\,{\left(-1+2\,k\right)!}^{6}}{{\left(-1+2\,k\right)}^{3}\,\left(3\,k\right)!\,{\left(1+4\,k\right)!}^{3}}}}$

${\displaystyle \zeta (3)={\tfrac {1}{64}}\sum _{k=0}^{\infty }(-1)^{k}{\frac {(205k^{2}+250k+77)\cdot k!^{10}}{(2k+1)!^{5}}}}$

${\displaystyle \zeta (3)={\tfrac {1}{24}}\sum _{k=0}^{\infty }(-1)^{k}{\frac {((2k+1)!(2k)!k!)^{3}(126392k^{5}+412708k^{4}+531578k^{3}+336367k^{2}+104000k+12463)}{(3k+2)!\cdot (4k+3)!^{3}}}}$

Некоторые из этих представлений были использованы для вычисления постоянной Апери со многими миллионами значащих цифр.

В 1998 году получено представление в виде ряда[11], которое даёт возможность вычислить произвольный бит постоянной Апери.

Существует также большое количество различных интегральных представлений для постоянной Апери, начиная от тривиальных формул типа

${\displaystyle \zeta (3)={\frac {1}{2}}\int \limits _{0}^{\infty }\!{\frac {x^{2}}{e^{x}-1}}\,dx={\frac {2}{3}}\int \limits _{0}^{\infty }\!{\frac {x^{2}}{e^{x}+1}}\,dx}$

или

${\displaystyle \zeta (3)=\int \limits _{0}^{1}\!{\frac {\ln(x)\ln(1-x)}{x}}\,dx}$

следующих из простейших интегральных определений дзета-функции Римана[12], до достаточно сложных, таких, как

${\displaystyle \zeta (3)=\pi \!\!\int \limits _{0}^{\infty }\!{\frac {\cos(2\,\mathrm {arctg} \,x)}{\left(x^{2}+1\right){\big [}\mathrm {ch} {\big (}{\frac {1}{2}}\pi x{\big )}{\big ]}^{2}}}\,dx\qquad }$ (Иоган Йенсен[13]),

${\displaystyle \zeta (3)=-{\frac {1}{2}}\int \limits _{0}^{1}\!\!\int \limits _{0}^{1}{\frac {\ln(xy)}{\,1-xy\,}}\,dx\,dy\qquad }$ (Фритс Бёкерс[14]),

${\displaystyle \zeta (3)=\,{\frac {8\pi ^{2}}{7}}\!\!\int \limits _{0}^{1}\!{\frac {x\left(x^{4}-4x^{2}+1\right)\ln \ln {\frac {1}{x}}}{\,(1+x^{2})^{4}\,}}\,dx\qquad }$ (Ярослав Благушин[15]).

Цепная дробь для константы Апери (последовательность A013631 в OEIS) выглядит следующим образом:

${\displaystyle \zeta (3)=[1;4,1,18,1,1,1,4,1,9,9,2,1,1,1,2,7,1,1,7,11,1,1,1,\cdots ]=}$

${\displaystyle =1+{\cfrac {1}{4+{\cfrac {1}{1+{\cfrac {1}{18+{\cfrac {1}{1+\ldots }}}}}}}}\;}$

Первую обобщённую цепную дробь для константы Апери, имеющую закономерность, открыли независимо Стилтьес и Рамануджан:

${\displaystyle \zeta (3)=1+{\cfrac {1}{4+{\cfrac {1^{3}}{1+{\cfrac {1^{3}}{12+{\cfrac {2^{3}}{1+{\cfrac {2^{3}}{20+{\cfrac {3^{3}}{1+{\cfrac {3^{3}}{28+{\cfrac {\dots }{\dots +{\cfrac {n^{3}}{1+{\cfrac {n^{3}}{4(2n+1)+\dots }}}}}}}}}}}}}}}}}}}}}$

Она может быть преобразована к виду:

${\displaystyle \zeta (3)=1+{\cfrac {1}{5-{\cfrac {1^{6}}{21-{\cfrac {2^{6}}{55-{\cfrac {3^{6}}{119-{\cfrac {4^{6}}{225-{\cfrac {\dots }{\dots +{\cfrac {n^{6}}{(2n^{3}+3n^{2}+11n+5)+\dots }}}}}}}}}}}}}}}$

Апери смог ускорить сходимость цепной дроби для константы:

${\displaystyle \zeta (3)={\frac {6}{5}}-{\cfrac {1^{6}}{117-{\cfrac {2^{6}}{535-{\cfrac {3^{6}}{1436-{\cfrac {4^{6}}{3105-{\cfrac {\dots }{\dots +{\cfrac {n^{6}}{(34n^{3}+51n^{2}+27n+5)+\dots }}}}}}}}}}}}}$[16][17]

Число известных значащих цифр постоянной Апери ${\displaystyle \zeta (3)}$ значительно выросло за последние десятилетия благодаря как увеличению компьютерных мощностей, так и улучшению алгоритмов[18].

Число известных значащих цифр постоянной Апери ${\displaystyle \zeta (3)}$

Дата	Количество значащих цифр	Авторы вычисления
1735	16	Леонард Эйлер[5][6]
1887	32	Томас Иоаннес Стилтьес
1996	520 000	Greg J. Fee & Simon Plouffe
1997	1 000 000	Bruno Haible & Thomas Papanikolaou
1997, май	10 536 006	Patrick Demichel
1998, февраль	14 000 074	Sebastian Wedeniwski
1998, март	32 000 213	Sebastian Wedeniwski
1998, июль	64 000 091	Sebastian Wedeniwski
1998, декабрь	128 000 026	Sebastian Wedeniwski[19]
2001, сентябрь	200 001 000	Shigeru Kondo & Xavier Gourdon
2002, февраль	600 001 000	Shigeru Kondo & Xavier Gourdon
2003, февраль	1 000 000 000	Patrick Demichel & Xavier Gourdon
2006, апрель	10 000 000 000	Shigeru Kondo & Steve Pagliarulo[20]
2009, январь	15 510 000 000	Alexander J. Yee & Raymond Chan[21]
2009, март	31 026 000 000	Alexander J. Yee & Raymond Chan[21]
2010, сентябрь	100 000 001 000	Alexander J. Yee[22]
2013, сентябрь	200 000 001 000	Robert J. Setti[22]
2015, август	250 000 000 000	Ron Watkins[22]
2015, декабрь	400 000 000 000	Dipanjan Nag[22]
2017, август	500 000 000 000	Ron Watkins[22]
2019, май	1 000 000 000 000	Ian Cutress[22]
2020, июль	1 200 000 000 000	Seungmin Kim[23]

Существует много исследований, посвящённых другим значениям дзета-функции Римана в нечётных точках ${\displaystyle \zeta (2n+1)}$ при ${\displaystyle n>1}$. В частности, в работах Вадима Зудилина и Тангая Ривоаля показано, что иррациональными является бесконечное множество чисел ${\displaystyle \zeta (2n+1)}$[24], а также что по крайней мере одно из чисел ${\displaystyle \zeta (5)}$, ${\displaystyle \zeta (7)}$, ${\displaystyle \zeta (9)}$, или ${\displaystyle \zeta (11)}$ является иррациональным[25].

• Ю. И. Манин, А. А. Панчишкин. I.2.4. Диофантовы приближения и иррациональность ζ(3) // Введение в теорию чисел. — ВИНИТИ, 1990. — Т. 49. — С. 83—89. — 341 с. — (Итоги науки и техники. Серия «Современные проблемы математики. Фундаментальные направления».).
• V. Ramaswami (1934), Notes on Riemann's ζ-function, J. London Math. Soc. Т. 9: 165–169, doi:10.1112/jlms/s1-9.3.165, <http://jlms.oxfordjournals.org/content/s1-9/3/165.full.pdf>
• Weisstein, Eric W. Apéry's constant (англ.) на сайте Wolfram MathWorld.