Полигамма-функция

Полига́мма-фу́нкция порядка m в математике определяется как (m+1)-я производная натурального логарифма гамма-функции,

\psi ^{(m)}(z)={\frac {{\rm {d}}^{m}}{{\rm {d}}z^{m}}}\psi (z)={\frac {{\rm {d}}^{m+1}}{{\rm {d}}z^{m+1}}}\ln \Gamma (z)\;,

Дигамма-функция

\psi (x)

Тригамма-функция

\psi '(x)

Тетрагамма-функция

\psi ''(x)

Пентагамма-функция

\psi '''(x)

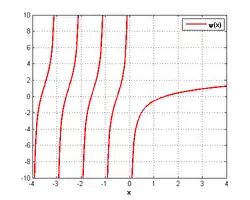
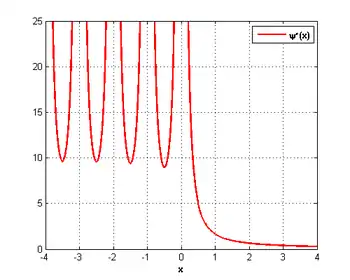
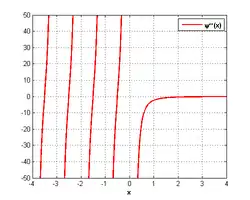
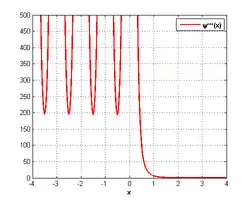
где $\Gamma (z)$ — гамма-функция, а

\psi (z)=\psi ^{(0)}(z)={\frac {\Gamma '(z)}{\Gamma (z)}}

— дигамма-функция[1], которую также можно определить через сумму следующего ряда:

\psi (z)=\psi ^{(0)}(z)=-\gamma +\sum \limits _{k=0}^{\infty }\left({\frac {1}{k+1}}-{\frac {1}{k+z}}\right)\;,

где ${\textstyle {\gamma }}$ — постоянная Эйлера—Маскерони. Это представление справедливо для любого комплексного $z\neq 0,\;-1,\;-2,\;-3,\ldots$ (в указанных точках функция ${\textstyle {\psi (z)}}$ имеет сингулярности первого порядка)[2].

Полигамма-функцию также можно определить через сумму ряда

\psi ^{(m)}(z)=(-1)^{m+1}\;m!\;\sum \limits _{k=0}^{\infty }\displaystyle {\frac {1}{(z+k)^{m+1}}}\;,\qquad m>0\;,

который получается из представления для дигамма-функции дифференцированием по z[1]. Это представление также справедливо для любого комплексного $z\neq 0,\;-1,\;-2,\;-3,\ldots$ (в указанных точках функция ${\textstyle {\psi ^{(m)}(z)}}$ имеет сингулярности порядка (m+1)). Оно может быть записано через дзета-функцию Гурвица[1],

\psi ^{(m)}(z)=(-1)^{m+1}\;m!\;\zeta (m+1,z)\;.

В этом смысле дзета-функция Гурвица может быть использована для обобщения полигамма-функции на случай произвольного (нецелого) порядка m.

Отметим, что в литературе ${\textstyle {\psi ^{(m)}(z)}}$ иногда обозначается как ${\textstyle {\psi _{m}(z)}}$ или явным образом указываются штрихи для производных по z. Функция ${\textstyle {\psi '(z)=\psi ^{(1)}(z)}}$ называется тригамма-функцией, ${\textstyle {\psi ''(z)=\psi ^{(2)}(z)}}$ — тетрагамма-функцией, ${\textstyle {\psi '''(z)=\psi ^{(3)}(z)}}$ — пентагамма-функцией, ${\textstyle {\psi ''''(z)=\psi ^{(4)}(z)}}$ — гексагамма-функцией, и т. д.

Интегральное представление

Полигамма-функция может быть представлена как

\psi ^{(m)}(z)=(-1)^{m+1}\int _{0}^{\infty }{\frac {t^{m}e^{-zt}}{1-e^{-t}}}{\rm {d}}t

Это представление справедливо для Re z >0 и m > 0. При m=0 (для дигамма-функции) интегральное представление может быть записано в виде

\psi (z)=\psi ^{(0)}(z)=-\gamma +\int _{0}^{\infty }{\frac {e^{-t}-e^{-zt}}{1-e^{-t}}}{\rm {d}}t=-\gamma +\int _{0}^{1}{\frac {1-t^{z-1}}{1-t}}{\rm {d}}t\;,

где ${\textstyle {\gamma }}$ — постоянная Эйлера—Маскерони.

Асимптотические разложения

При $z\to \infty \;$ ( $\;|\operatorname {arg} \;{z}|<\pi$ ) справедливо следующее разложение с использованием чисел Бернулли:

\psi ^{(m)}(z)=(-1)^{m-1}\left[{\frac {(m-1)!}{z^{m}}}+{\frac {m!}{2z^{m+1}}}+\sum _{k=1}^{\infty }{\frac {(2k+m-1)!\;B_{2k}}{(2k)!\;z^{2k+m}}}\right]

Разложение в ряд Тейлора вблизи аргумента, равного единице, имеет вид

\psi ^{(m)}(z+1)=\sum _{k=0}^{\infty }(-1)^{m+k+1}(m+k)!\;\zeta (m+k+1)\;{\frac {z^{k}}{k!}}\;,

где ζ обозначает дзета-функцию Римана. Этот ряд сходится при |z| < 1, и он может быть получен из соответствующего ряда для дзета-функции Гурвица.

Частные значения

Значения полигамма-функции при целых и полуцелых значениях аргумента выражаются через дзета-функцию Римана,

\psi ^{(m)}(1)=(-1)^{m+1}m!\;\zeta (m+1)\;,\qquad m>0

\psi ^{(m)}({\tfrac {1}{2}})=(-1)^{m+1}m!\;(2^{m+1}-1)\;\zeta (m+1)\;,\qquad m>0\;,

а для дигамма-функции (при m=0) —

\psi (1)=\psi ^{(0)}(1)=-\gamma \;,

\psi ({\tfrac {1}{2}})=\psi ^{(0)}({\tfrac {1}{2}})=-\gamma -2\ln {2}\;,

где ${\textstyle {\gamma }}$ — постоянная Эйлера—Маскерони[1].

Чтобы получить значения полигамма-функции при других целых (положительных) и полуцелых значениях аргумента, можно использовать рекуррентное соотношение, приведённое ниже.

Другие формулы

Полигамма-функция удовлетворяет рекуррентному соотношению[1]

\psi ^{(m)}(z+1)=\psi ^{(m)}(z)+{\frac {(-1)^{m}\;m!}{z^{m+1}}}\;,

а также формуле дополнения[1]

\psi ^{(m)}(1-z)+(-1)^{m+1}\;\psi ^{(m)}(z)=(-1)^{m}\pi {\frac {{\rm {d}}^{m}}{{\rm {d}}z^{m}}}\cot(\pi z)\;.

Для полигамма-функции кратного аргумента существует следующее свойство[1]:

\psi ^{(m)}(kz)={\frac {1}{k^{m+1}}}\sum _{n=0}^{k-1}\psi ^{(m)}\left(z+{\frac {n}{k}}\right),\qquad m>0

а для дигамма-функции ( $m=0$ ) к правой части надо добавить lnk[1],

\psi (kz)=\ln {k}+{\frac {1}{k}}\sum _{n=0}^{k-1}\psi \left(z+{\frac {n}{k}}\right).

См. также

Примечания

Eric W. Weisstein. Polygamma Function (англ.) на сайте Wolfram MathWorld.
Eric W. Weisstein. Digamma Function (англ.) на сайте Wolfram MathWorld.

Ссылки

Milton Abramowitz, Irene A. Stegun. §6.4 Polygamma Functions // Handbook of Mathematical Functions (англ.). — New York: Dover Publications, 1964. — ISBN 0-486-61272-4.
Weisstein, Eric W. Polygamma Function (англ.) на сайте Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[PGF-1] Eric W. Weisstein. Polygamma Function (англ.) на сайте Wolfram MathWorld.

[DGF-2] Eric W. Weisstein. Digamma Function (англ.) на сайте Wolfram MathWorld.