Тригамма-функция
Тригамма-функция в математике является второй из полигамма-функций. Она обозначается и определяется как
где — гамма-функция[1]. Из этого определения следует, что
где — дигамма-функция (первая из полигамма-функций)[2].
Тригамма-функцию можно также определить через сумму следующего ряда:
откуда видно, что она является специальным случаем дзета-функции Гурвица (англ. Hurwitz zeta-function)[2],
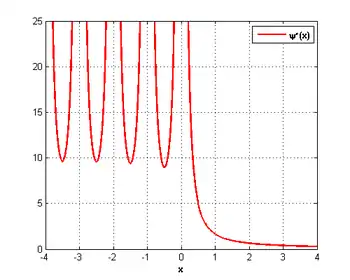
Эти формулы верны, когда (в указанных точках функция имеет квадратичные сингулярности, см. график функции).
Существуют также другие обозначения для , используемые в литературе:
Иногда термин «тригамма-функция» употребляется для функции [1].
Интегральные представления
Используя представление в виде ряда, а также формулу для суммы членов геометрической прогрессии, можно получить следующее двойное интегральное представление:
С помощью интегрирования по частям получается следующее однократное представление:
Используется также другое представление, которое может быть получено из предыдущего заменой x = e—t:
Другие формулы
Тригамма-функция удовлетворяет рекуррентному соотношению[2]
а также формуле дополнения[2]
Для тригамма-функции кратного аргумента существует следующее свойство[2]:
Приведём также асимптотическое разложение с использованием чисел Бернулли:
Частные значения
Ниже приведены частные значения тригамма-функции[1]:
где G — постоянная Каталана, а — функция Клаузена, связанная с мнимой частью дилогарифма через
Используя формулу кратного аргумента и формулу дополнения, a также связь с функцией Клаузена[3][4], получаем:
Для значений за пределами интервала можно использовать рекуррентное соотношение, приведённое выше. Например[1],
Примечания
- Eric W. Weisstein. Trigamma Function (англ.) на сайте Wolfram MathWorld.
- Eric W. Weisstein. Polygamma Function (англ.) на сайте Wolfram MathWorld.
- C.C. Grosjean, Formulae concerning the computation of the Clausen integral , J. Comp. Appl. Math. 11 (1984) 331—342
- P.J. de Doelder, On the Clausen integral and a related integral, J. Comp. Appl. Math. 11 (1984) 325—330
Ссылки
- Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. См. раздел §6.4
- Eric W. Weisstein, Trigamma Function, MathWorld — mathworld.wolfram.com
- Eric W. Weisstein, Polygamma Function, MathWorld — mathworld.wolfram.com