Дигамма-функция

В математике дига́мма-фу́нкция ${\textstyle {\psi (x)}}$ определяется как логарифмическая производная гамма-функции:

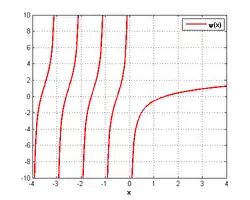
\psi (x)={\frac {d}{dx}}\ln {\Gamma (x)}={\frac {\Gamma '(x)}{\Gamma (x)}}.

Дигамма-функция

\psi (x)

Она является полигамма-функцией первого порядка, а полигамма-функции высших порядков (тригамма-функция и т.д.) получаются из неё дифференцированием.

Свойства

Дигамма-функция связана с гармоническими числами соотношением
$\displaystyle {\psi (n)=H_{n-1}-\gamma },$

где

{\textstyle {H_{n}}}

— n-е гармоническое число, а

{\textstyle {\gamma }}

Формула дополнения
$\displaystyle {\psi (1-x)-\psi (x)=\pi \operatorname {ctg} (\pi x)}$
Рекуррентное соотношение
$\psi (x+1)=\psi (x)+{\frac {1}{x}}$
Разложение в бесконечную сумму
$\psi (x)=\ln x-{\frac {1}{2x}}+\sum _{n=1}^{\infty }{\frac {\zeta (1-2n)}{x^{2n}}}$

где

\zeta (x)

Логарифмическое разложение
$\psi (x)=\sum _{n=0}^{\infty }{\frac {1}{n+1}}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}\ln(x+k)$
Теорема Гаусса
${\frac {\Gamma '(p/q)}{\Gamma (p/q)}}=-\gamma -\ln(2q)-{\frac {\pi }{2}}\operatorname {ctg} \left({\frac {\pi p}{q}}\right)+2\sum _{0<n<q/2}\cos \left({\frac {2\pi pn}{q}}\right)\ln \sin \left({\frac {\pi n}{q}}\right)$

при целых

p,q

с условием

0<p<q

.

Для всех $z\neq -1,-2,-3,\ldots$ справедливо разложения в ряд:
$\psi (z+1)=-\gamma +\sum _{n=1}^{\infty }{\frac {z}{n(n+z)}}.$

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.