Дилогарифм
Дилогари́фм — специальная функция в математике, которая обозначается и является частным случаем полилогарифма при . Дилогарифм определяется как
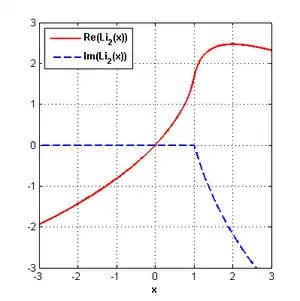
Приведённое определение дилогарифма верно для комплексных значений переменной . Для действительных значений у этой функции есть разрез вдоль действительной оси от до . Обычно значение функции на разрезе определяется так, что мнимая часть дилогарифма отрицательна:
Функцию часто называют дилогарифмом Эйлера, в честь Леонарда Эйлера, который рассмотрел эту функцию в 1768 году[1]. Иногда дилогарифм называют функцией Спенса (Spence's function) или интегралом Спенса[2] в честь шотландского математика Уильяма Спенса (William Spence, 1777—1815)[3], который в начале XIX века исследовал функции, соответствующие и . Название "дилогарифм" было введено Хиллом (C.J. Hill) в 1828 году.
Функциональные соотношения
Для дилогарифма существует ряд полезных функциональных соотношений,
Для действительных ,
Известны также соотношения, содержащие две независимые переменные — например, тождество Хилла:
Частные значения
Используя соотношение между функциями от и , получаем
Существует также ряд результатов для аргументов, связанных с золотым сечением ,
а также для дилогарифма мнимого аргумента,
где — постоянная Каталана.
Соотношения для частных значений
Функции, связанные с дилогарифмом
- Функция Клаузена
- Возникает при рассмотрении дилогарифма, аргумент которого находится на единичной окружности в комплексной плоскости,
- Таким образом,
- Функция Лобачевского
- Эта функция используется при вычислении объёмов в гиперболической геометрии, и она связана с функцией Клаузена (а следовательно и с дилогарифмом),
- Иногда используется другое определение функции Лобачевского,
- Интегральный арктангенс
- Возникает при рассмотрении дилогарифма мнимого аргумента,
- Таким образом,
- Эта функция выражается через дилогарифмы как
- В частности, .
Примечания
Ссылки
- Leonard Lewin,. Dilogarithms and associated functions. — Macdonald, London, 1958. MR: 0105524
- Leonard Lewin,. Polylogarithms and associated functions. — North Holland, New York, Oxford, 1981.
- Don Zagier, The dilogarithm function (PDF)
- Weisstein, Eric W. Dilogarithm (англ.) на сайте Wolfram MathWorld.
