Полюс (комплексный анализ)
Изолированная особая точка называется полюсом функции , голоморфной в некоторой проколотой окрестности этой точки, если существует предел
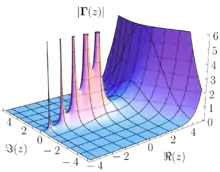
Модуль Гамма-функции . Слева (Re z<0) у функции есть полюса, в них она стремится к бесконечности. Справа (Re z>0) полюсов нет, функция всюду конечна.
.
Критерии полюса
- Точка является полюсом тогда, и только тогда, когда в разложении функции в ряд Лорана в проколотой окрестности точки главная часть содержит конечное число отличных от нуля членов, то есть
,
где — правильная часть ряда Лорана. Если , то называется полюсом порядка . Если , то полюс называется простым.
- Точка является полюсом порядка тогда и только тогда, когда , а
- Точка является полюсом порядка тогда и только тогда, когда она является для функции нулем порядка .
См. также
- Другие типы изолированных особых точек:
Литература
- Бицадзе А.В. Основы теории аналитических функций комплексного переменного — М., Наука, 1969.
- Шабат Б. В., Введение в комплексный анализ — М., Наука, 1969.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.