Биномиальный коэффициент
В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «число сочетаний из n по k», читается «C из n по k»):
| (1) |
для натуральных степеней .
Биномиальные коэффициенты могут быть также определены для произвольных действительных показателей . В случае произвольного действительного числа биномиальные коэффициенты определяются как коэффициенты разложения выражения в бесконечный степенной ряд:
где в случае неотрицательных целых n все коэффициенты при k > n обращаются в нуль и поэтому данное разложение представляет собой конечную сумму (1).
В комбинаторике биномиальный коэффициент для неотрицательных целых чисел n и k интерпретируется как количество сочетаний из n по k, то есть как количество всех (нестрогих) подмножеств (выборок) размера k в n-элементном множестве.
Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Явные формулы
Вычисляя коэффициенты в разложении в степенной ряд, можно получить явные формулы для биномиальных коэффициентов .
Для всех действительных чисел n и целых чисел k:
где обозначает факториал числа k.
Для неотрицательных целых n и k также справедливы формулы:
Для целых отрицательных показателей коэффициенты разложения бинома равны
Треугольник Паскаля

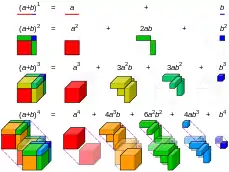
Тождество
позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:
Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от той, что выписана здесь, поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).
Если в каждой строке треугольника Паскаля все числа разделить на (это сумма всех чисел в строке), то все строки при стремлении n к бесконечности примут вид функции нормального распределения.
Свойства
Производящие функции
Для фиксированного значения n производящей функцией последовательности биномиальных коэффициентов … является
Для фиксированного значения k производящая функция последовательности коэффициентов … равна
Двумерной производящей функцией биномиальных коэффициентов для целых является:
- или
Делимость
Из теоремы Люка следует, что:
- коэффициент нечётен в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули;
- коэффициент некратен простому числу p в p-ичной записи числа k все разряды не превосходят соответствующих разрядов числа n;
- в последовательности биномиальных коэффициентов :
- все числа не кратны заданному простому p число представимо в виде , где натуральное число m < p;
- все числа, кроме первого и последнего, кратны заданному простому p ;
- количество нечётных чисел равно степени двойки, показатель которой равен количеству единиц в двоичной записи числа n;
- чётных и нечётных чисел не может быть поровну;
- количество чисел, не кратных простому p, равно , где числа — разряды p-ичной записи числа n; а число где — функция «пол», — это длина данной записи.
Основные тождества
- (правило симметрии).
- (вынесение за скобки).
- (замена индексов).
- .
Бином Ньютона и следствия
- где
- где
- Более сильное тождество: где
а более общем виде
Свёртка Вандермонда и следствия
- (свёртка Вандермонда), где а
Это тождество получается вычислением коэффициента при в разложении с учётом тождества Сумма берётся по всем целым , для которых Для произвольных действительных , число ненулевых слагаемых в сумме будет конечно.
- .
- Более общее тождество: , если .
Другие тождества
- — n-е гармоническое число.
- Мультисекция ряда даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t в виде конечной суммы из s слагаемых:

- Имеют место равенства[1]:
Откуда следует:
где — количество размещений из n по k.
Матричные соотношения
Если взять квадратную матрицу, отсчитав N элементов по катетам треугольника Паскаля и повернув матрицу на любой из четырёх углов, то детерминант этих четырёх матриц равен ±1 при любом N, причём детерминант матрицы с вершиной треугольника в верхнем левом углу равен 1.
В матрице числа на диагонали i + j = const повторяют числа строк треугольника Паскаля (i, j = 0,1,…). Её можно разложить в произведение двух строго диагональных матриц: нижнетреугольной и получаемой из неё транспонированием. А именно:
где . Обратная матрица к U имеет вид:
Таким образом, можно разложить обратную матрицу к в произведение двух строго диагональных матриц: первая матрица — верхнетреугольная, а вторая получается из первой путём транспонирования, что позволяет дать явное выражение для обратных элементов:
- , где i, j , m, n = 0..p.
Элементы обратной матрицы меняются при изменении её размера и, в отличие от матрицы , недостаточно приписать новую строку и столбец. Столбец j матрицы есть многочлен степени j по аргументу i, следовательно, первые p столбцов образуют полный базис в пространстве векторов длины p+1, чьи координаты могут быть интерполированы многочленом равной или меньшей степени p-1. Нижняя строка матрицы ортогональна любому такому вектору.
- при , где многочлен степени a.
Если произвольный вектор длины можно интерполировать многочленом степени , то скалярное произведение со строками (нумерация с 0) матрицы равно нулю. Используя тождество выше и равенство единицы скалярного произведения нижней строки матрицы на последний столбец матрицы , получаем:
Для показателя большего p можно задать рекуррентную формулу:
где многочлен
Для доказательства сперва доказывается тождество:
Если требуется найти формулу не для всех показателей степени, то
Старший коэффициент равен 1, потребуется a-1 значений, чтобы найти другие коэффициенты:
- для
Асимптотика и оценки
- при (неравенство Чебышёва).
- , при (энтропийная оценка), где — энтропия.
- (неравенство Чернова).
Непосредственно из формулы Стирлинга следует, что для верно .
Целозначные полиномы
Биномиальные коэффициенты … являются целозначными полиномами от , т.е. принимают целые значения при целых значениях — это нетрудно понять, например, по треугольнику Паскаля. Более того, они образуют базис целозначных полиномов, в котором все целозначные полиномы выражаются как линейные комбинации с целыми коэффициентами.[2]
В то же время стандартный базис … не позволяет выразить все целочисленные полиномы, если использовать только целые коэффициенты, так как уже имеет дробные коэффициенты при степенях .
Этот результат обобщается на полиномы многих переменных. А именно, если полином степени имеет вещественные коэффициенты и принимает целые значения при целых значениях переменных, то
где — полином с целыми коэффициентами.[3]
Алгоритмы вычисления
Биномиальные коэффициенты можно вычислить с помощью рекуррентной формулы , если на каждом шаге n хранить значения при Этот алгоритм особенно эффективен, если нужно получить все значения при фиксированном . Алгоритм требует памяти ( при вычислении всей таблицы биномиальных коэффициентов) и времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени), где — «o» большое.
При фиксированном значении k биномиальные коэффициенты могут быть вычислены по рекуррентной формуле с начальным значением . Для вычисления значения этот метод требует памяти и времени.
Если требуется вычислить коэффициенты при фиксированном значении можно воспользоваться формулой при начальном условии . При каждом шаге итерации числитель уменьшается на (начальное значение равно ), а знаменатель соответственно увеличивается на (начальное значение — ). Для вычисления значения этот метод требует памяти и времени.
См. также
Примечания
- Четырёхмерные таблицы в комбинаторике — два странных способа посчитать сочетания. habr.com (30 ноября 2020). Дата обращения: 27 марта 2021.
- Прасолов В. В. Глава 12. Целозначные многочлены // Многочлены. — М.: МЦНМО, 1999, 2001, 2003.
- Ю. Матиясевич. Десятая проблема Гильберта. — Наука, 1993.
Литература
- Биномиальные коэффициенты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17—25.
- Кузьмин О. В. Треугольник и пирамида Паскаля: свойства и обобщения // Соросовский Образовательный Журнал. — 2000. — Т. 6, № 5. — С. 101—109.
- Ландо С. К. Теневое исчисление // VIII летняя школа «Современная математика». — Дубна, 2008.
- Винберг Э. Б. Удивительные арифметические свойства биномиальных коэффициентов // Математическое просвещение. — 2008. — Вып. 12. — С. 33–42.
- Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Математические основы информатики = Concrete Mathematics. A Foundation for Computer Science. — 2-е. — М.: Мир; Бином. Лаборатория знаний; «Вильямс», 1998 — 2009. — 703, 784 с. — ISBN 95-94774-560-7, 78-5-8459-1588-7.