Неравенство Чебышёва
Нера́венство Чебышёва (или неравенство Бьенеме — Чебышёва) — неравенство в теории меры и теории вероятностей. Оно было первый раз получено Бьенеме в 1853 году, и позже также Чебышёвым.
Неравенство, использующееся в теории меры, является более общим, в теории вероятностей используется его следствие.
Неравенство Чебышёва в теории меры
Неравенство Чебышёва в теории меры описывает взаимосвязь интеграла Лебега и меры. Аналог этого неравенства в теории вероятностей — неравенство Маркова. Неравенство Чебышёва также используется для доказательства вложения пространства в слабое пространство .
Формулировки
- Пусть — пространство с мерой. Пусть также
- — суммируемая на функция
- .
- Тогда справедливо неравенство:
- .
- В более общем виде:
- Если — неотрицательная вещественная измеримая функция, неубывающая на области определения , то
- В терминах пространства :
- Пусть . Тогда
Неравенство Чебышёва может быть получено, как следствие из неравенства Маркова.
Неравенство Чебышёва в теории вероятностей
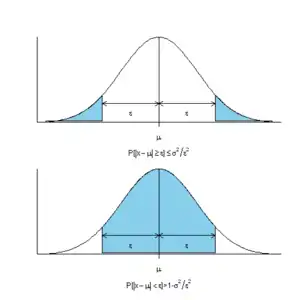
Неравенство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения, близкие к своему среднему. А более точно, оно даёт оценку вероятности того, что случайная величина примет значение, далёкое от своего среднего.
Неравенство Чебышёва является следствием неравенства Маркова.
Формулировки
Пусть случайная величина определена на вероятностном пространстве , а её математическое ожидание и дисперсия конечны. Тогда
- ,
где .
Если , где — стандартное отклонение и , то получаем
- .
В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на стандартных отклонения, с вероятностью меньше . Отклоняется от среднего на стандартных отклонения с вероятностью меньше . Иными словами, случайная величина укладывается в стандартных отклонения с вероятностью и в стандартных отклонения с вероятностью
Для важнейшего случая одномодальных распределений неравенство Высочанского — Петунина существенно усиливает неравенство Чебышёва, включая в себя дробь 4/9. Таким образом, граница в стандартных отклонения включает значений случайной величины. В отличие от нормального распределения, где стандартных отклонения включают значений случайной величины.
См. также
Литература
- Колмогоров, А. Н., Фомин, С. В. Элементы теории функций и функционального анализа. — изд. четвёртое, переработанное. — М.: Наука, 1976. — 544 с.