Брунново зацепление

В теории узлов брунново зацепление — это нетривиальное зацепление, которое распадается при удалении любой компоненты. Другими словами, разрезание любого (топологического) кольца расцепляет все остальные кольца (стало быть, никакие два из колец не сцеплены, как в зацеплении Хопфа).

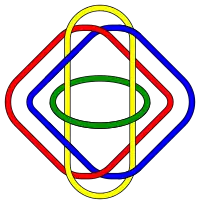
Это зацепление из четырёх компонент брунново.
Брунново зацепление с шестью компонентами.

Название брунново дано в честь Германа Брунна, который в статье 1892 года Über Verkettung привёл примеры таких зацеплений.

Примеры
Кольца Борромео являются простейшим брунновым зацеплением.

Наиболее известным и самым простым брунновым зацеплением являются кольца Борромео, зацепление трёх колец. Однако для любого числа, начиная с трёх, существует бесконечное число брунновых зацеплений, содержащее такое число колец. Существует несколько относительно простых зацеплений из трёх компонент, которые не эквивалентны кольцам Борромео:

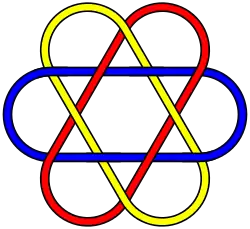  • Зацепление с 12 пересечениями.
  • Зацепление с 18 пересечениями.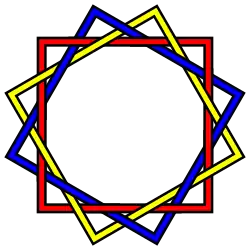
  • Зацепление с 24 пересечениями.

Простейшее брунново зацепление, отличное от колец Борромео (имеющих 6 пересечений), по-видимому, зацепление L10a140 с 10 пересечениями[1].

Пример n-компонентного бруннова зацепления — это брунново зацепление «резиновых колец», где каждая компонента оборачивает предыдущую по схеме aba−1b−1 и последнее кольцо зацепляется за первое, образуя цикл.

Классификация

Брунновы зацепления описаны с точностью до гомотопии Джоном Милнором в статье 1954 года [2], и инварианты, введённые им, теперь называются инвариантами Милнора

(n + 1)-компонентное зацепление можно понимать как элемент группы зацепления n незацеплённых компонент (группа зацепления в этом случае является фундаментальной группой дополнения зацепления). Группа зацепления n незацеплённых компонент является свободным произведением n образующих, то есть свободной группой Fn.

Не любой элемент группы Fn порождает брунново зацепление. Милнор показал, что группа элементов, соответствующих брунновым зацеплениям, связана с градуированной алгеброй Ли нижнего центрального ряда свободной группы, и её можно понимать как «соотношения» в свободной алгебре Ли.

Произведения Масси

Брунновы зацепления можно понимать с помощью произведений Масси: произведение Масси — это n-членное произведение, которое определено только если все (n − 1)-членные произведения обращаются в нуль. Это соответствует свойству бруннова зацепления, в котором все наборы из (n − 1) компонент не сцеплены, но все n компонент вместе образуют нетривиальное зацепление.

Брунновы косы
Обычная коса является брунновой — при удалении чёрной нити синяя оказывается над красной так, что они оказываются расцеплёнными. То же самое происходит при удалении других нитей.

Бруннова коса — это коса, которая становится тривиальной при удалении любой из её нитей. Брунновы косы образуют подгруппу в группе кос. Брунновы косы на сфере, не являющиеся брунновыми на (плоском) круге, дают нетривиальные элементы в группах гомотопий сферы. Например, «стандартная» коса, соответствующая кольцам Борромео, даёт расслоение Хопфа S3 → S2, и продолжение такого плетения также даёт бруннову косу.

Примеры из реального мира

Многие головоломки на распутывание и некоторые механические головоломки являются вариантами брунновых зацеплений, и их целью является освобождение какого-либо элемента, частично связанного с остальной частью головоломки.

Брунновы цепочки используются для создания декоративных украшений из резиновых колец с помощью устройств типа Wonder Loom (или её варианта Rainbow Loom).

Примечания
  1. Dror Bar-Natan (2010-08-16). «All Brunnians, Maybe», [Academic Pensieve].
  2. Milnor, 1954.

Литература
  • A. J. Berrick, Frederick R. Cohen, Yan Loi Wong, Jie Wu. Configurations, braids, and homotopy groups // Journal of the American Mathematical Society. — 2006. — Т. 19, вып. 2. — С. 265–326. — doi:10.1090/S0894-0347-05-00507-2..
  • Hermann Brunn, «Über Verkettung», J. Münch. Ber, XXII. 77-99 (1892). JFM 24.0507.01  (нем.)
  • John Milnor. Link Groups // Annals of Mathematics. — Annals of Mathematics, 1954. — Т. 59, вып. 2 (March). — С. 177–195. — doi:10.2307/1969685. — .
  • Dale Rolfsen (1976). Knots and Links. Berkeley: Publish or Perish, Inc. ISBN 0-914098-16-0.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.