Простой узел (теория узлов)

В теории узлов простой узел или простое зацепление — узел, который, в определённом смысле, неразложим. Точнее, это нетривиальный узел, который нельзя представить в виде конкатенации двух нетривиальных узлов. Об узлах, не являющихся простыми, говорят как о составных узлах или составных зацеплениях. Определить, является ли данный узел простым или нет, может оказаться сложной задачей.

Эта статья о классе математических узлов, не разложимых на части; о простейшем виде узлов на верёвках см. Простой узел.

Примеры

Хорошим примером семейства простых узлов служат торические узлы. Эти узлы образуются накручиванием окружности на тор p раз в одном направлении и q раз в другом, где p и q являются взаимно простыми целыми числами.

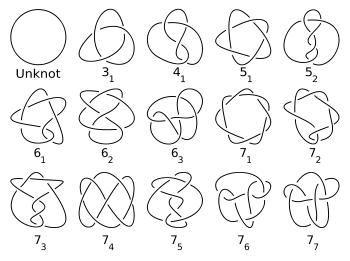
Простейший простой узел — это трилистник с тремя пересечениями. Трилистник является, фактически, (2, 3)-торическим узлом. Узел «восьмёрка» с четырьмя пересечениями является простейшим неторическим узлом. Для любого положительного целого числа n имеется конечное число простых узлов с n пересечениями. Первые несколько значений числа простых узлов (последовательность A002863 в OEIS) даны в следующей таблице.

n 12345678910111213141516
Число простых узлов
с n пересечениями		 001123721491655522176998846 972253 2931 388 705
Составные узлы 00000214............
Всего 001125825............

Заметим, что антиподы считались в этой таблице и ниже лежащем рисунке только один раз (т. е. узел и его зеркальное отражение считаются эквивалентными).

Изображения всех простых узлов с семью и менее пересечениями без учёта зеркальных отражений. (Тривиальный узел простым не считается)

Теорема Шуберта

Теорема, принадлежащая Хорсту Шуберту, утверждает, что любой узел можно единственным образом представить в виде конкатенации простых узлов[1].

См. также
  • Список простых узлов

Примечания
  1. Schubert, 1949, с. 57—104.

Литература
  • H. Schubert. Die eindeutige Zerlegbarkeit eines Knotens in Primknoten // S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. — 1949.

Ссылки
  • Weisstein, Eric W. Prime Knot (англ.) на сайте Wolfram MathWorld.
  • [Prime Links with a Non-Prime Component ]Knot Atlas
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.