Мутация (теория узлов)

В теории узлов мутация — это операция над узлом, которая может привести к другому узлу.

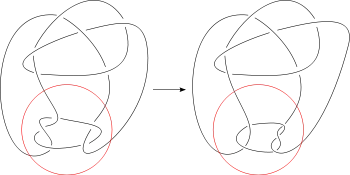
Узел Киношита–Терасака (11n42) и узел Конвея (11n34) связаны мутацией.

Определение

Пусть K — узел, заданный в виде диаграммы. Пусть D — диск в плоскости диаграммы, границы которого пересекают K ровно четыре раза. Можно считать (в случае необходимости используем изотопию), что диск геометрически круглый и четыре точки пересечения расположены на равном расстоянии. Часть узла внутри диска является клубком. Имеется два отражения, которые меняют местами пары конечных точек этого клубка. Кроме того, имеются также вращения. Мутация заменяет исходный клубок на клубок, полученный любой из этих операций. В результате всегда получим узел, который называется мутацией узла K[1].

Мутанты нелегко отличить, поскольку они имеют много тех же инвариантов[2]. Они имеют тот же гиперболический объём (как показал Руберман) и тот же многочлен HOMFLY.

Примеры
  • Пара узлов, Конвея и Киношиты-Терасака, являются мутациями друг друга, но имеют различный род, равный 3 и 2 соответственно.

Примечания
  1. Livingston, 1993, с. 214.
  2. Cromwell, 1964, с. 177—181.

Литература
  • Charles Livingston. Knot theory. — Washington DC: The Mathematical Association of America, 1993. — Т. 24. — (The Carus Mathematical Monographs). — ISBN 088385-027-3.
  • Peter R. Cromwell. Knots and Links. — Cambridge: Cambridge University Press, 1964. — ISBN 0-521-83947-5, 0-521-54831-4.
  • Colin Adams. The Knot Book. — New York: W. H. Freeman and Company. — ISBN 0-8050-7380-9.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.