Сателлитный узел
Сателлитный узел — конструкция позволяющая построить новый узел из двух узлов с определёнными дополнительными структурами. Эта конструкция включает связную сумму узлов а также удвоение Уайтхеда как частные случаи.

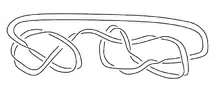
Построение
Сателлитный узел можно описать следующим образом: начните с нетривиальныого узла лежащего внутри незаузленного полнотория . «Нетривиальный» означает, что не может лежать в шаре вложенном в и не изотопен центральной кривой полнотория. Затем завязать полноторие в нетривиальный узел. То есть существуют нетривиальное вложение , такое, что и . При этом образ центральной кривой полнотория называется компаньёном .
Обычно дополнительно предполагают, что вложение раскрученно, то есть не меняют индекс зацепления двух окружностей в .
История
В 1949 году Хорст Шуберт доказал[1], что каждый ориентированный узел в разлагается в связную сумму узлов и это разложение единственно с точностью до перестановки. Вскоре после этого, он понял, что может дать новое доказательство этой теоремы в анализируя несжимаемые торы, в дополнении к связной сумме. Это привело его к исследованию общих несжимаемых торов в дополнении узла, и к определению сателлитного узла[2]
См. также
Примечания
- Schubert, H. Die eindeutige Zerlegbarkeit eines Knotens in Primknoten. S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), 57–104.
- Schubert, H. Knoten und Vollringe. Acta Math. 90 (1953), 131–286.