Группа кос

Группа кос была впервые явно описана Эмилем Артином в 1925 году.[1]

Рассмотрим случай n = 4, из этого примера легко будет понять, что представляет собой произвольная группа кос. Рассмотрим две параллельные прямые (на рисунке они расположены вертикально), на каждой из которых лежит по четыре пронумерованные точки, так что точки с одинаковыми номерами находятся друг против друга. Разобьём точки на пары и с помощью нитей соединим их. Если изобразить получившуюся картинку в плоскости, некоторые нити могут проходить друг под другом (можно считать, что нити всегда пересекаются трансверсально). При этом важно учитывать порядок следования нитей в точке пересечения:

отличается от

С другой стороны, две такие конфигурации, которые можно сделать одинаковыми перемещением нитей, не затрагивающим конечные точки, мы будем считать одинаковыми:

не отличается от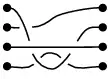

Все нити должны быть направлены слева направо, то есть каждая из нитей может пересекать вертикальную прямую (параллельную прямым с пронумерованными точками) не более чем в одной точке:

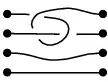не является косой.

Для двух кос можно рассмотреть их композицию, нарисовав вторую рядом с первой, то есть склеив соответствующие четыре концевые точки:

×

=

Группа B₄ — это фактор множества всех таких конфигураций на четырёх парах точек по отношению эквивалентности, заданному непрерывными преобразованиями плоскости, на котором указанным выше способом задана групповая операция. Данная операция удовлетворяет всем аксиомам группы; в частности, нейтральный элемент — класс эквивалентности четырёх параллельных нитей и для каждого элемента обратный к нему можно получить симметрией относительно вертикальной прямой.

Строго формализовать данное выше описание можно несколькими способами:

• Геометрический способ использует понятие гомотопии, а именно, B_n определяется как фундаментальная группа пространства n-точечных подмножеств на плоскости с естественной топологией.
• Также можно дать чисто алгебраическое описание, задав образующие и соотношения.
  • Например, B_n можно задать (n − 1) образующими и ${\displaystyle {\tfrac {n\cdot (n-1)}{2}}}$ соотношениями:

    ${\displaystyle B_{n}=\langle \sigma _{1},\ldots ,\sigma _{n-1}\ \mid \ \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1}\ {\text{при}}\ 1\leq i\leq n-2\ {\text{и}}\ \sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\ {\text{for}}\ |i-j|\geq 2\rangle$ :}

В частности, любой элемент B₄ можно записать как композицию следующих трёх элементов (и обратных к ним):

σ1	σ2	σ3

Чтобы понять, почему это интуитивно очевидно, «просканируем» картинку, перемещая вертикальную прямую слева направо. Всякий раз, когда i-я сверху (на данной прямой) нить проходит под (i + 1)-й, будем писать σ_i, а если над (i + 1)-й, то σ_i⁻¹.

Очевидно, что выполняется соотношение σ₁σ₃ = σ₃σ₁, тогда как чуть более трудно увидеть, что σ₁σ₂σ₁ = σ₂σ₁σ₂ (убедиться в этом проще всего, нарисовав линии на листке бумаги).

Можно доказать, что все соотношения между элементами группы кос следуют из соотношений такого вида.

• Группа B₁ тривиальна, B₂ бесконечна (как и все последующие группы кос) и изоморфна Z, B₃ изоморфна группе узла трилистника.
• Все элементы B_n, кроме нейтрального, имеют бесконечный порядок; то есть B_n не имеет кручения.
• Существует сюръективный гомоморфизм B_n → S_n из группы кос в группу перестановок. Действительно, каждому элементу группы B_n можно сопоставить перестановку множества n вершин, при которой левому концу каждой «нити» сопоставляется правый её конец.
  • Ядро этого гомоморфизма называется группой крашеных кос, она обычно обозначается ${\displaystyle P_{n}}$.
  • Для групп крашеных кос существует короткая точная последовательность

    ${\displaystyle F_{n-1}\to P_{n}\to P_{n-1},}$

  где ${\displaystyle F_{n-1}}$ обозначает свободную группу с ${\displaystyle n-1}$ образующей.

• Группу кос можно определить как группу классов отображений диска с выколотыми точками. Точнее, группа кос с n нитями естественным образом изоморфна группе классов преобразований диска n выколотыми точками.

• Deligne, Pierre (1972), Les immeubles des groupes de tresses généralisés, Inventiones Mathematicae Т. 17 (4): 273–302, ISSN 0020-9910, DOI 10.1007/BF01406236
• Birman, Joan, and Brendle, Tara E., «Braids: A Survey», revised 26 February 2005. In Menasco and Thistlethwaite.
• Carlucci, Lorenzo; Dehornoy, Patrick; and Weiermann, Andreas, «Unprovability results involving braids», 23 November 2007
• Kassel, Christian; and Turaev, Vladimir, Braid Groups, Springer, 2008. ISBN 0-387-33841-1
• Menasco, W., and Thistlethwaite, M., (editors), Handbook of Knot Theory, Amsterdam : Elsevier, 2005. ISBN 0-444-51452-X

• CRAG: CRyptography and Groups at Algebraic Cryptography Center Contains extensive library for computations with Braid Groups
• P. Fabel, Completing Artin’s braid group on infinitely many strands, Journal of Knot Theory and its Ramifications, Vol. 14, No. 8 (2005) 979—991
• P. Fabel, The mapping class group of a disk with infinitely many holes, Journal of Knot Theory and its Ramifications, Vol. 15, No. 1 (2006) 21-29
• Chernavskii, A.V. (2001), "Braid theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Java-приложение, моделирующее группу B₅.
• C. Nayak and F. Wilczek’s connection of projective braid group representations to the fractional quantum Hall effect
• Presentation for FradkinFest by C. V. Nayak
• N. Read’s criticism of the reality of Wilczek-Nayak representation