Теорема синусов
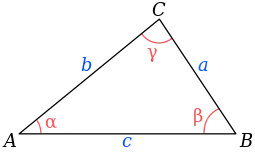
Теоре́ма си́нусов — теорема, устанавливающая зависимость между длинами сторон треугольника и величиной противолежащих им углов. Существуют два варианта теоремы; обычная теорема синусов:
|
Стороны треугольника пропорциональны синусам противолежащих углов. |
и расширенная теорема синусов:
|
Для произвольного треугольника где , , — стороны треугольника, — соответственно противолежащие им углы, а — радиус окружности, описанной около треугольника. |
Доказательства
Доказательство обычной теоремы синусов
Воспользуемся только определением высоты треугольника, опущенной на сторону b, и синуса для двух углов:
- . Следовательно, , что и требовалось доказать. Повторив те же рассуждения для двух других сторон треугольника, получаем окончательный вариант обычной теоремы синусов. ∎
Доказательство расширенной теоремы синусов
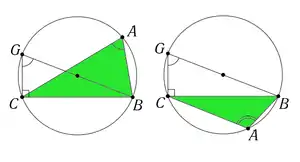
Достаточно доказать, что
Проведем диаметр для описанной окружности. По свойству углов, вписанных в окружность, угол прямой, а угол равен либо , если точки и лежат по одну сторону от прямой , либо в противном случае. Поскольку , в обоих случаях получаем
- .
Повторив то же рассуждение для двух других сторон треугольника, получаем:
Вариации и обобщения
В треугольнике против большего угла лежит бо́льшая сторона, против большей стороны лежит больший угол.
где — угол между гранями и ; — общая грань и ; — объём симплекса.
История
- В первой главе Альмагеста (около 140 года н. э.) теорема синусов используется, но явно не формулируется[1].
- Древнейшее из дошедших до нас доказательств теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике» написанной в XIII веке[2].
- Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в X веке[3]. В труде Ал-Джайяни XI века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере[4].
Вариации и обобщения
- Сферическая теорема синусов
- На плоскости Лобачевского с кривизной теорема синусов принимает следующую форму:
Примечания
- Florian Cajori. A History of Mathematics (англ.). — 5th edition. — 1991. — P. 47.
- Berggren, J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (англ.). — Princeton University Press, 2007. — P. 518. — ISBN 9780691114859.
- Sesiano just lists al-Wafa as a contributor. Sesiano, Jacques (2000). «Islamic mathematics», pp. 137. — Page 157, in Selin, Helaine & D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 1402002602
- Abu Abd Allah Muhammad ibn Muadh Al-Jayyani
