Редко используемые тригонометрические функции
Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К ним относятся:
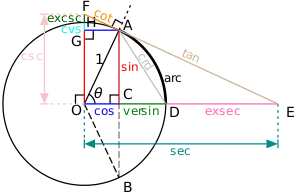

- Синус-верзус (другие написания: версинус, синус версус, называется также «стрелка дуги»). Определяется как Представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Иногда используются обозначения
- Косинус-верзус (другие написания: коверсинус, косинус версус). Определяется как Иногда используются обозначения
- Гаверсинус (лат. haversinus, сокращение от half the versed sine). Определяется как Используется также обозначение
- Гаверкосинус (лат. havercosinus, сокращение от half the versed cosine). Определяется как Используется также обозначение
- Эксеканс (лат. exsecant) или экссеканс. Определяется как
- Экскосеканс — дополнительная функция к эксекансу:
Использование
Версинус, коверсинус и гаверсинус были удобны для ручных расчётов с использованием логарифмов, поскольку они всюду неотрицательны, однако в связи с развитием вычислительных средств эта область применения неактуальна. В настоящее время эти функции используются для описания соответствующих сигналов в электронике (например, в функциональных генераторах). Гаверсинус также используется в навигационных расчётах для избежания ошибок округления в вычислительных системах с ограниченной разрядностью.
Синус-верзус
Определение
Синус-верзус определён через синус и косинус как
Синус-верзус вместе с косинусом составляет радиус окружности.
Свойства
Версинус — периодическая функция с периодом . Версинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная версинуса
Первообразная версинуса
Косинус-верзус
Свойства
Веркосинус — периодическая функция с периодом . Веркосинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная веркосинуса
Первообразная веркосинуса
Гаверсинус
Свойства
Гаверсинус — периодическая функция с периодом . Гаверсинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная гаверсинуса
Первообразная гаверсинуса
Гаверкосинус
Свойства
Гаверкосинус — периодическая функция с периодом . Гаверкосинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная гаверкосинуса
Первообразная гаверкосинуса
Эксеканс
Определение
Эксеканс определён через секанс как
Свойства
Эксеканс — периодическая функция с периодом . Эксеканс определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.
Производная эксеканса
Первообразная эксеканса
Экскосеканс
Определение
Экскосеканс определён через эксеканс и косеканс как
Свойства
Экскосеканс — периодическая функция с периодом . Экскосеканс определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.
можно использовать в плоскости комплексных чисел.