Теорема котангенсов
Теорема котангенсов — тригонометрическая теорема, связывающая радиус вписанной окружности треугольника с длиной его сторон. Теорему котангенсов удобно использовать при решении треугольника по трём сторонам.
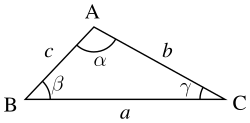
Общий вид треугольника
Формулировка
Пусть
- — длины трёх сторон треугольника,
- — углы, лежащие напротив, соответственно, сторон ,
- — радиус вписанной окружности треугольника и
- — полупериметр треугольника.
Тогда справедливы следующие формулы:[1]
- ,
- ,
- ,
или эквивалентно:
- .
Словами теорему можно сформулировать так: котангенс половинного угла равен отношению полупериметра минус длина противолежащей стороны указанного угла к радиусу вписанной окружности.
Обобщение
В сферической тригонометрии существует похожая формула для половины угла, а также двойственная к ней формула половины стороны.
Следствия
Из теоремы котангенсов может быть получено выражение для радиуса вписанной окружности . Далее, так как площадь треугольника , из теоремы котангенсов следует формула Герона.
См. также
Примечания
- The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
