Теорема о внешнем угле треугольника

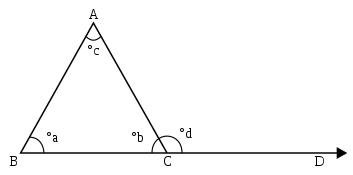
Внешним углом плоского треугольника при данной вершине называется угол, смежный с внутренним углом треугольника при этой вершине (см. рис.). Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины.

• Внешний угол равен разности между 180° и внутренним углом, он может принимать значения от 0 до 180° не включительно.
• Теорема о внешнем угле треугольника: Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом. Иными словами, (см. рис.): ${\displaystyle d=a+c.}$

Утверждение теоремы следует из теоремы о сумме углов треугольника, равной 180°.

Пусть ABC — произвольный треугольник с внешним углом d. Так как углы b и d — смежные, то их сумма равна 180°, то есть угол d = 180° — b. По теореме о сумме углов треугольника, угол b = 180° — (a + c). Из этого следует, что углы a + c = 180 — b. Так как d также равен 180 — b, то угол d = a + c. Что и требовалось доказать.

С другой стороны, если выполняется Теорема о внешнем угле треугольника, тогда справедливы следующая логическая цепь равенств:

${\displaystyle d=a+c}$

${\displaystyle b+d=180^{\circ }=>}$

${\displaystyle b+a+c=180^{\circ }.}$.

Иллюстрация к евклидовому доказательству теоремы о внешнем угле треугольника

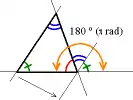
В евклидовом доказательстве теоремы о внешнем угле треугольника, принадлежащем Евклиду, (а также и результата о том, то сумма всех трех внутренних углов треугольника равна 180°) сначала проводится прямая, параллельна стороне AB, проходящая через вершину C, а затем, используя свойство соответственных углов при двух параллельных прямых и одной секущей и о внутренних накрест лежащих углах при двух параллельных прямых, требуемое утверждение получают как иллюстрацию (см. рис.).[1].

Теорема о внешнем угле треугольника используется тогда, когда пытаются вычислить меры неизвестных углов в геометрии, в задачах с многоугольниками, где используются треугольники.

• Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1
• Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN 0-7167-0454-4
• Heath, Thomas L. The Thirteen Books of Euclid's Elements (неопр.). — 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925]. — New York: Dover Publications, 1956.

(3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3).

• Henderson, David W. & Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.), Pearson/Prentice-Hall, ISBN 0-13-143748-8
• Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3
• Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill
• Wheater, Carolyn C. (2007), Homework Helpers: Geometry, Franklin Lakes, NJ: Career Press, с. 88–90, ISBN 978-1-56414-936-7