Теорема Чевы
Теорема Чевы — классическая теорема аффинной геометрии и геометрии треугольника. Установлена в 1678 году итальянским инженером Джованни Чевой.
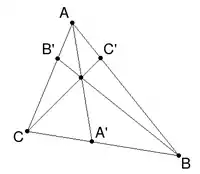
Формулировка
Определим чевиану как отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне.
Три чевианы треугольника проходят через одну точку тогда и только тогда, когда:
Замечания
Эта теорема является аффинной, то есть она может быть сформулирована с использованием только тех свойств, которые сохраняются при аффинных преобразованиях.
Вариации и обобщения

Теорема Чевы для точек, лежащих на продолжениях сторон. Чевианы и их основания обозначены зелёным цветом, а точка их пересечения — голубым.
- Эту теорему можно обобщить на случай, когда точки лежат на продолжениях сторон . Для этого надо воспользоваться «отношением направленных отрезков». Оно определено для двух коллинеарных направленных отрезков и и обозначается
- Пусть лежат на прямых треугольника . Прямые конкурентны (то есть параллельны или пересекаются в одной точке) тогда и только тогда, когда:
- Теорема Понселе. Исходную теорему Чевы можно обобщить на случай многоугольника с нечетным числом сторон. Тогда ее называют теоремой Понселе. Она звучит так: прямые, соединяющие какую-нибудь точку с вершинами многоугольника, имеющего нечетное число сторон, образуют на противоположных его сторонах такие отрезки, что произведение отрезков, не имеющих общих концов, равно произведению остальных отрезков (см. п. 23, с 35. в [1])
- Тригонометрическая теорема Чевы:
- При этом углы здесь считаются ориентированными; то есть есть угол, на который надо повернуть прямую против часовой стрелки, чтоб получить прямую .
О доказательствах
Известны доказательства
- методом площадей,
- с помощью геометрии масс,
- двойное применение теоремы Менелая и многие другие.
Сам Чева привёл доказательство с помощью геометрии масс, но существует также и другие доказательства.
См. также
Литература
- Балк М. Б., Болтянский В. Г. Геометрия масс. — М.: Наука, 1987. —(Библиотечка «Квант»)).
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.: МЦНМО, 2002.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 66—68. — ISBN 5-94057-170-0.
- Шаль, Мишель. О сочинении Чевы, под заглавием: De lineis rectis se invicem secantibus, statica constructio (in — 4°, Milan, 1678). // Исторический обзор происхождения и развития геометрических методов. Т. 2. М., 1883.
- Giovanni Ceva. De lineis rectis se invicem secantibus, statica constructio Milan, 1678
Примечания
- Зетель С. И. Новая геометрия треугольника. 2-е изд. М.: Учпедгиз, 1962. 153 с.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.