Метод площадей
Метод площадей — метод решения геометрических тождеств путём подсчёта площадей фигур разными способами.
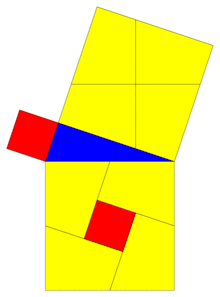
Классическим примером применения метода площадей являются доказательство Евклида теоремы Пифагора приведённое ниже.. Методом площадей доказываются также теорема о биссектрисе, теорема Чевы и многие другие.
Доказательство Евклида
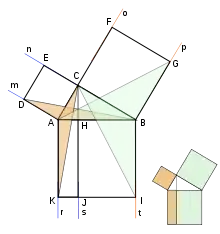
Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.
Конструкция, используемая для доказательства следующая: для прямоугольного треугольника с прямым углом , квадратов над катетами и и квадрата над гипотенузой строится высота и продолжающий её луч , разбивающий квадрат над гипотенузой на два прямоугольника и . Доказательство нацелено на установление равенства площадей прямоугольника с квадратом над катетом ; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.
Равенство площадей прямоугольника и устанавливается через конгруэнтность треугольников и , площадь каждого из которых равна половине площади квадратов и соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямой угла и угла при .
Таким образом, доказательством устанавливается, что площадь квадрата построенного на гипотенузе, составленного из прямоугольников и , равна сумме площадей квадратов над катетами.
Литература
- 9.3 в И.Ф. Шарыгин. Геометрия 7—9,. — М.: Дрофа, 1997. — 352 с.