Центр вписанной окружности

Центр вписанной окружности
Центр вписанной окружности
	; Окружность, вписанная в треугольник
Барицентрические координаты
Трилинейные координаты	1:1:1
Код ЭЦТ	X(1)
Связанные точки
Изогонально сопряженная	она же
Дополнительная	центр Шпикера
Антидополнительная	точка Нагеля
	Медиафайлы на Викискладе

Центр вписанной окружности треугольника (инцентр) — одна из замечательных точек треугольника, точка пересечения биссектрис треугольника. Центр вписанной в треугольник окружности также иногда называют инцентром.

Традиционно обозначается латинской буквой $I$ (по первой букве английского слова "Incenter"). В энциклопедии центров треугольника зарегистрирован под символом $X(1)$ .

Свойства

Центр вписанной окружности треугольника находится на одинаковом расстоянии от всех сторон треугольника.

Для треугольника $\triangle ABC$ со сторонами $a$ , $b$ и $c$ , противолежащими вершинам $A$ , $B$ и $C$ соответственно, инцентр делит биссектрису угла $A$ в отношении:
${\frac {b+c}{a}}$ .

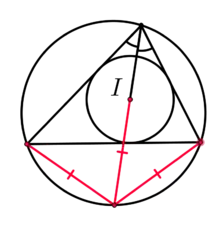
Теорема трилистника

Если продолжение биссектрисы угла $B$ пересекает описанную окружность $\triangle ABC$ в точке $D$ , то выполняется равенство: $DA=DC=DI=DJ$ , где $J$ — центр вневписанной окружности, касающейся стороны $AC$ ; это свойство инцентра известно как теорема трилистника (также — лемма о трезубце, теорема Клайнэра).

Расстояние между инцентром $I$ и центром описанной окружности $O$ выражается формулой Эйлера:
$OI^{2}=R^{2}-2Rr$ ,

где

R

и

r

— радиусы описанной и вписанной окружностей соответственно.

Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[1].

Инцентр можно найти как центр масс вершин треугольника если в каждую вершину поместить массу, равную длине противолежащей стороны (см. также Центр Шпикера).

Инцентр данного треугольника является точкой Нагеля треугольника, образованного его 3 средними линиями (серединного треугольника).[2]

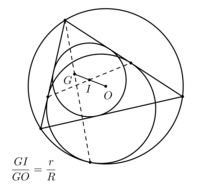
Полувписанная окружность и центр гомотетии G для вписанной и описанной окружностей с радиусами соответственно r и R. Лемма Веррьера: Центр вписанной окружности лежит на отрезке, соединяющем точки касания сторон треугольника и окружности Веррьера (полувписанной окружности)

Лемма Веррьера[3]. Точки касания окружностей Веррьера (полувписанных окружностей) со сторонами лежат на прямой, которая проходит через центр вписанной окружности (инцентр) (См. серый рис. снизу).

Теорема Ригби. Если к любой стороне остроугольного треугольника провести высоту и касающуюся ее с другой стороны вневписанную окружность, то точка касания последней с этой стороной, середина упомянутой высоты, а также инцентр лежат на одной прямой.[4].

- Из теоремы Ригби следует, что 3 отрезка, соединяющих середину каждой из 3 высот треугольника с точкой касания вневписанной окружности, проведенной к той же стороне, что и высота, пересекаются в инцентре.

Теорема Тебо 3

Третья теорема Тебо. Пусть $ABC$ — произвольный треугольник, $D$ — произвольная точка на стороне $BC$ , $I_{1}$ — центр окружности, касающейся отрезков $AD,BD$ и описанной около $\Delta ABC$ окружности, $I_{2}$ — центр окружности, касающейся отрезков $CD,AD$ и описанной около $\Delta ABC$ окружности. Тогда отрезок $I_{1}I_{2}$ проходит через точку $I$ — центр окружности, вписанной в $\Delta ABC$ , и при этом $I_{1}I:II_{2}=\operatorname {tg} ^{2}{\frac {\phi }{2}}$ , где $\phi =\angle BDA$ .

См. также

Примечания

Мякишев А. Г. . Элементы геометрии треугольника. — М.: МЦНМО, 2002. — 32 с. — (Библиотека «Математическое просвещение». вып. 19). — ISBN 5-94057-048-8. — С. 11, п. 5.
Honsberger, R.. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer. 1995. P. 51, Пункт (b).// https://b-ok.cc/book/447019/c8c303
Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с.
Ross Honsberger, "3. An Unlikely Collinearity" in "Episodes in Nineteenth and Twentieth Century Euclidean Geometry" (Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390), p. 30, Figure 34

Литература

Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 88-90. — 383 с. — ISBN 5-09-001287-3.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Мякишев А. Г. . Элементы геометрии треугольника. — М.: МЦНМО, 2002. — 32 с. — (Библиотека «Математическое просвещение». вып. 19). — ISBN 5-94057-048-8. — С. 11, п. 5.

[2] Honsberger, R.. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer. 1995. P. 51, Пункт (b).// https://b-ok.cc/book/447019/c8c303

[3] Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с.

[4] Ross Honsberger, "3. An Unlikely Collinearity" in "Episodes in Nineteenth and Twentieth Century Euclidean Geometry" (Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390), p. 30, Figure 34

Треугольник
Виды треугольников	Прямоугольный Равнобедренный Равносторонний Равнобедренный прямоугольный
Замечательные линии в треугольнике	Медиана Высота Биссектриса Серединный перпендикуляр Средняя линия Описанная и вписанная окружности Прямая Симсона Прямая Эйлера Симедиана Чевиана
Замечательные точки треугольника	Ортоцентр Центроид Инцентр Точка Брокара Точка Вектена Точка Жергонна Точка Лемуана Точка Микеля Точка Нагеля Точки Наполеона Точки Торричелли Центр окружности девяти точек Центр Шпикера Энциклопедия центров треугольника
Основные теоремы	Неравенство треугольника Признаки подобия треугольников Решение треугольников Теорема о внешнем угле треугольника Теорема о сумме углов треугольника Теорема Пифагора Теорема косинусов Теорема синусов Теорема о проекциях Формула Герона
Дополнительные теоремы	Теорема Ван-Обеля Теорема Менелая Теорема Ройшле (Теркема) Теорема Стюарта Теорема тангенсов Теорема котангенсов Теорема Чевы Формулы Мольвейде
Обобщения	Сферический треугольник Гиперболический треугольник Симплекс