Точка Нагеля
Точка Нагеля — точка пересечения отрезков, соединяющих вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями.
| Точка Нагеля | |
|---|---|
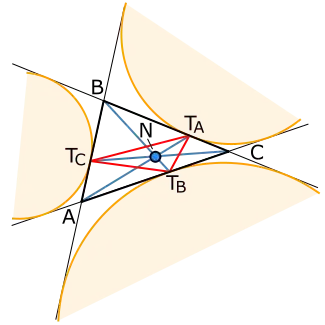 N — точка Нагеля треугольника ABC | |
| Барицентрические координаты | |
| Трилинейные координаты | |
| Код ЭЦТ | X(8) |
| Связанные точки | |
| Изотомически сопряженная | точка Жергона |
| Дополнительная | центр вписанной окружности |
Обычно обозначается .
Свойства

- Точка Нагеля лежит на одной прямой с инцентром и центроидом, при этом центроид делит отрезок между точкой Нагеля и инцентром в отношении 2 : 1. Эта прямая называется прямой Нагеля (см. рисунок).
- Если точки , , таковы, что каждый из отрезков , и делит периметр треугольника пополам, то эти отрезки пересекаются в одной точке — точке Нагеля.
- Точка Нагеля изотомически сопряжена точке Жергонна.
- Точка Нагеля изогонально сопряжена с центром положительной гомотетии вписанной и описанной окружности (точка Веррьера).
- Расстояние между ортоцентром и точкой Нагеля равно диаметру окружности Фурмана и равно
- .
- Половине этого расстояния равно расстояние между центром описанной окружности и инцентром[1].
- Чевиану точки Нагеля в английской литературе иногда называют сплиттером (splitter) или делителем пополам периметра. К сплиттеру они относят и кливер треугольника.
- Инцентр данного треугольника является точкой Нагеля треугольника, образованного его 3 средними линиями (серединного треугольника).[2][3]
Треугольник Нагеля
* Треугольник Нагеля (см. рис. выше) для треугольника определяется вершинами , и , которые являются точками касания вневписанных окружностей треугольника и точка противоположна стороне , и т. д.
Свойства
- Описанная вокруг треугольника окружность называется окружностью Мандарта (частный случай эллипса Мандарта).
- Три прямые , и делят периметр пополам и пересекаются в одной точке Нагеля — X(8).
- Перпендикуляры, восстановленные в трех вершинах треугольника Нагеля к сторонам основного треугольника (то есть в точках касания вневписанных окружностей со сторонами основного треугольника), пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности[4].
- Анимацию построения точки Нагеля см. на рис.
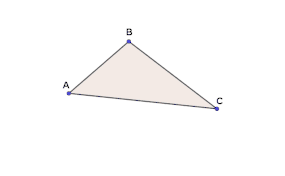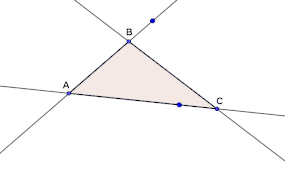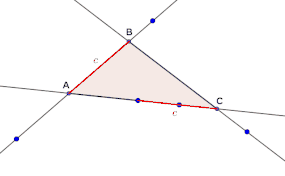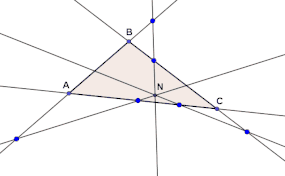
Анимация построения точки Нагеля
Замечание
Точка Нагеля относится к слабым точкам. Поэтому следует говорить не об одной, а о нескольких точках Нагеля. То есть, соединение других точек касания вневписанных окружностей с вершинами треугольника дает ещё три точки Нагеля.
История
Названа по имени Христиана Генриха фон Нагеля, впервые охарактеризовавшего её в статье 1836 г.
См. также
Примечания
- Weisstein, Eric W. Fuhrmann Circle (англ.) на сайте Wolfram MathWorld.
- Honsberger, R.. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer. 1995. P. 51, Пункт (b).// https://b-ok.cc/book/447019/c8c303
- Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, p. 247, 1929.
- Мякишев А. Г. Элементы геометрии треугольника. — М.: МЦНМО, 2002. — С. 11, п. 5. — (Библиотека «Математическое просвещение»).
Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.