Треугольник точек касания вневписанных окружностей
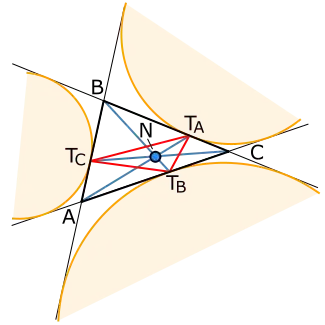
Треугольник точек касания вневписанных окружностей треугольника образован соединением точек, в которых вневписанные окружности касаются треугольника. Для краткости в статье будем называть этот треугольник треугольником внекасаний.
Координаты
Вершины треугольника внекасаний задаются трилинейными координатами:
Или, эквивалентно, если a,b,c являются длинами сторон, противоположных углам A, B, C соответственно,
Связанные фигуры
Разделителями периметра треугольника являются отрезки, соединяющие вершины исходного треугольника с соответствующими вершинами треугольника внекасаний. Они делят периметр пополам (это и есть определение разделителя периметра) и пересекаются в точке Нагеля, которая на рисунке выделена синим цветом и помечена буквой «N».
Эллипс Мандара касается сторон исходного треугольника в трёх вершинах треугольника внекасаний[1].
Площадь
Площадь треугольника внекасаний, , задаётся формулой:
- ,
где , , являются площадью, радиусом вписанной окружности и полупериметром исходного треугольника, а , , являются длинами сторон исходного треугольника.
Это та же площадь, что и у треугольника касаний[2].
Примечания
- Juhász, 2012, с. 37–46.
- Weisstein, Eric W. "Extouch Triangle." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ExtouchTriangle.html
Литература
- Imre Juhász. Control point based representation of inellipses of triangles // Annales Mathematicae et Informaticae. — 2012. — Т. 40. — С. 37–46.