Эллипс Мандара

Эллипс Манда́ра — вписанный в заданный треугольник эллипс, касающийся его сторон в точках касания их с вневписанными окружностями[1].

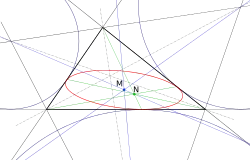
Эллипс Мандара (красный) вписан в треугольник (чёрный) в точках касания сторон с вневписанными окружностями (серые). Линии, проходящие через точку Нагеля ${\displaystyle N}$ — зелёные; линии, проходящие через центр эллипса ${\displaystyle M}$ — голубые.

Назван по имени французского математика Мандара (H. Mandart), опубликовавшего исследования этого объекта в 1893—1894 годах[2][3].

Центр эллипса Мандара — одна из замечательных точек треугольника (нем. mittenpunkt), найдена Нагелем в 1836 году как точка пересечения симедиан треугольника, образованного центрами его вневписанных окружностей[4][5]. В Энциклопедии центров треугольника точке присвоен идентификатор ${\displaystyle X(9)}$.

Для вписанных коник вписанный эллипс Мандара описывается параметрами:

${\displaystyle x:y:z={\frac {a}{b+c-a}}:{\frac {b}{a+c-b}}:{\frac {c}{a+b-c}}}$,

где ${\displaystyle a}$, ${\displaystyle b}$ и ${\displaystyle c}$ — стороны данного треугольника.