Вписанная и вневписанные в треугольник окружности

Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника.

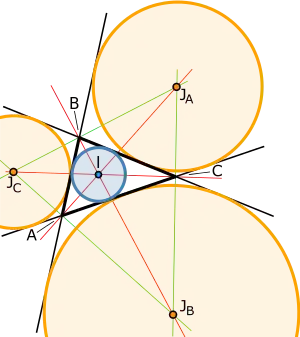
Треугольник (чёрный) с вписанной окружностью (синей), инцентр (I), вневписанными окружностями (оранжевые), эксцентры (J_A,J_B,J_C), внутренние биссектрисы (красные) и внешние биссектрисы (зелёные)

Вневписанная окружность треугольника — окружность, лежащая вне треугольника и касающаяся одной стороны треугольника и продолжения двух других сторон. Любой треугольник имеет три различные вневписанные окружности, каждая из которых касается своей стороны треугольника. Центром вневписанной окружности является пересечение биссектрисы одного внутреннего угла и биссектрис двух других внешних углов. Поскольку биссектриса внутреннего угла перпендикулярна биссектрисе смежного внешнего угла, центр вписанной окружности вместе с тремя центрами вневписанных окружностей образуют ортоцентричную систему[1].

Не все многоугольники с числом сторон более трёх имеют вписанную окружность. Те, которые имеют, называются описанными.

Некоторые сокращения

Вместо слов "вписанная (внутрь треугольника)" и "вневписанная (вне треугольника) окружности" возможно использование соответственно сокращений: "внуокружность" и "внеокружность" [2] по аналогии с английскими сокращениями соответственно вписанной и вневписанной в треугольник окружностей: Incircle и Excircle. Центры соответствующих окружностей кратко называют "внуцентр" и "внецентр" [2] по аналогии с английскими сокращениями соответственно центров вписанной и вневписанной в треугольник окружностей: Incenter и Excenter.
С учетом того, что вместо слова "окружность" возможно использование синонимов: обод (круга), обод круга,- "внуокружность" и "внеокружность" будут кратко называться соответственно, как "внуобод" (круга) и "внеобод" (круга) [2].

Связь с площадью треугольника

Радиусы вписанных и вневписанных окружностей имеют тесную связь с площадью треугольника.[3]

Вписанная окружность

Пусть $\triangle ABC$ имеет вписанную окружность радиуса r с центром I. Пусть a — длина BC, b — длина AC, а c — длина AB. Пусть вписанная окружность касается AB в некоторой точке C′, тогда $\angle AC'I$ является прямым. Тогда радиус C’I будет высотой треугольника $\triangle IAB$ . Таким образом, $\triangle IAB$ имеет основание длины c и высоту r, а следовательно, его площадь равна ${\tfrac {1}{2}}cr$ . Подобным же образом $\triangle IAC$ имеет площадь ${\tfrac {1}{2}}br$ и $\triangle IBC$ имеет площадь ${\tfrac {1}{2}}ar$ . Поскольку эти три треугольника разбивают $\triangle ABC$ , получаем, что

\Delta ={\frac {1}{2}}(a+b+c)r=pr,

где $\Delta$ — площадь $\triangle ABC$ , а $p={\frac {1}{2}}(a+b+c)$ — его полупериметр.

Чтобы получить альтернативную формулу, рассмотрим $\triangle IC'A$ . Это прямоугольный треугольник, у которого один из катетов равен r, а другой равен $r\cdot \mathrm {ctg} {\frac {\angle A}{2}}$ . То же самое верно для $\triangle IB'A$ . Весь треугольник состоит из 6 таких треугольников, и общая площадь составляет:

\Delta =r^{2}\cdot (\mathrm {ctg} {\frac {\angle A}{2}}+\mathrm {ctg} {\frac {\angle B}{2}}+\mathrm {ctg} {\frac {\angle C}{2}})

Вневписанные окружности

Пусть вневписанная окружность, касающаяся стороны AB, касается продолжения стороны AC в точке G, и пусть радиус этой окружности равен $r_{c}$ , а её центр — $I_{c}$ . Тогда $I_{c}G$ является высотой треугольника $\triangle ACI_{c}$ , так что $\triangle ACI_{c}$ имеет площадь ${\tfrac {1}{2}}br_{c}$ . По тем же причинам $\triangle BCI_{c}$ имеет площадь ${\tfrac {1}{2}}ar_{c}$ , а $\triangle ABI_{c}$ имеет площадь ${\tfrac {1}{2}}cr_{c}$ . Тогда

\Delta ={\frac {1}{2}}(a+b-c)r_{c}=(p-c)r_{c}

.

Таким образом, ввиду симметрии,

\Delta =pr=(p-a)r_{a}=(p-b)r_{b}=(p-c)r_{c}

.

По теореме косинусов получаем

\cos A={\frac {b^{2}+c^{2}-a^{2}}{2bc}}

Комбинируя это с тождеством $\sin ^{2}A+\cos ^{2}A=1$ , получим

\sin A={\frac {\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}{2bc}}

Но $\Delta ={\tfrac {1}{2}}bc\sin A$ , так что

{\begin{aligned}\Delta &={\frac {1}{4}}{\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}\\&={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\\&={\sqrt {p(p-a)(p-b)(p-c)}},\end{aligned}}

и это формула Герона вычисления площади треугольника по его сторонам.

Комбинируя формулу Герона с $pr=\Delta$ , получим

r^{2}={\frac {\Delta ^{2}}{p^{2}}}={\frac {(p-a)(p-b)(p-c)}{p}}

.

Аналогично, $(p-a)r_{a}=\Delta$ даёт

r_{a}^{2}={\frac {p(p-b)(p-c)}{p-a}}

.

Из этих формул видно, что вневписанные окружности всегда больше вписанной и наибольшая окружность соответствует самой длинной стороне, а самая наименьшая из вневписанных окружностей соответствует самой маленькой стороне. Дальнейшее комбинирование формул приводит к:[4]

\Delta ={\sqrt {rr_{a}r_{b}r_{c}}}.

Отношение площади вписанной окружности к площади треугольника меньше или равно ${\frac {\pi }{3{\sqrt {3}}}}$ , и равенство достигается только на правильных треугольниках.[5]

Окружность девяти точек и точка Фейербаха

Теорема Эйлера об окружности Эйлера. Середины отрезков высот от ортоцентра до вершин треугольника называются точками Эйлера. Основания медиан, основания высот и точки Эйлера лежат на одной окружности, называемой окружностью девяти точек.[6]

Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности в четырёх разных точках. Одна из них - точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.

Треугольник и точка Жергонна

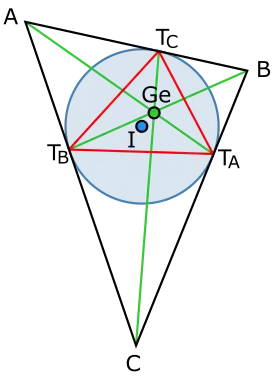
Треугольник ΔABC с вписанной окружностью (синяя), и её центр (синий, I), треугольник точек касания (красный, ΔT_aT_bT_c) и точка Жергонна (зелёная, Ge)

Треугольник Жергонна (для треугольника ABC) определяется тремя точками касания вписанной окружности на трёх сторонах. Эти вершины обозначим T_A, и т. д.. Точка T_A лежит напротив вершины A.

Этот треугольник Жергонна T_AT_BT_C известен также как треугольник касаний треугольника ABC.

Три прямые AT_A, BT_B и CT_C пересекаются в одной точке — точке Жергонна и обозначается Ge — X(7). Точка Жергонна лежит внутри открытого ортоцентроидного круга с выколотым центром.[7]

Интересно, что точка Жергонна треугольника является точкой пересечения симедиан треугольника Жергонна. Полный набор свойств точки Жергонна можно найти в статье Декова.[8]

Трилинейные координаты вершин треугольника касаний задаются формулами

вершина $A=0:\sec ^{2}\left({\frac {B}{2}}\right):\sec ^{2}\left({\frac {C}{2}}\right)$
вершина $B=\sec ^{2}\left({\frac {A}{2}}\right):0:\sec ^{2}\left({\frac {C}{2}}\right)$
вершина $C=\sec ^{2}\left({\frac {A}{2}}\right):\sec ^{2}\left({\frac {B}{2}}\right):0$

Трилинейные координаты точки Жергонна

\sec ^{2}\left({\frac {A}{2}}\right):\sec ^{2}\left({\frac {B}{2}}\right):\sec ^{2}\left({\frac {C}{2}}\right)

,

или, эквивалентно, по теореме синусов,

{\frac {bc}{b+c-a}}:{\frac {ca}{c+a-b}}:{\frac {ab}{a+b-c}}

.

Точка Жергонна является изотомическим сопряжением точки Нагеля.

Треугольник и точка Нагеля

Треугольник Нагеля (см. рис. выше) для треугольника ABC определяется вершинами T_A, T_B и T_C, которые являются точками касания вневписанных окружностей треугольника ABC и точка X_A противоположна стороне A, и т. д. Описанная вокруг треугольника T_AT_BT_C окружность называется окружностью Мандарта (частный случай эллипса Мандарта). Три прямые AT_A, BT_B и CT_C делят периметр пополам и пересекаются в одной точке Нагеля Na — X(8).

Трилинейные координаты точек касания треугольника вневписанными окружностями задаются формулами

вершина $A=0:\csc ^{2}\left({\frac {B}{2}}\right):\csc ^{2}\left({\frac {C}{2}}\right)$
вершина $B=\csc ^{2}\left({\frac {A}{2}}\right):0:\csc ^{2}\left({\frac {C}{2}}\right)$
вершина $C=\csc ^{2}\left({\frac {A}{2}}\right):\csc ^{2}\left({\frac {B}{2}}\right):0$

Трилинейные координаты точки Нагеля задаются формулами

\csc ^{2}\left({\frac {A}{2}}\right):\csc ^{2}\left({\frac {B}{2}}\right):\csc ^{2}\left({\frac {C}{2}}\right)

,

или, эквивалентно, по теореме синусов,

{\frac {b+c-a}{a}}:{\frac {c+a-b}{b}}:{\frac {a+b-c}{c}}

.

Точка Нагеля является изотомическим сопряжением точки Жергонна.

Трилинейные координаты вписанных треугольников

Трилинейные координаты вершин треугольника, образованного основаниями биссектрис, задаются формулами

вершина $A=0:1:1$
вершина $B=1:0:1$
вершина $C=1:1:0$

Трилинейные координаты треугольника, образованного точками касания сторон внеописанными окружностями, задаются формулами

вершина $A=-1:1:1$
вершина $B=1:-1:1$
вершина $C=1:-1:-1$

Уравнения окружностей

Пусть x : y : z — координаты точки в трилинейных координатах, и пусть u = cos²(A/2), v = cos²(B/2), w = cos²(C/2). Четыре окружности, описанные выше, можно задать любым из двух указанных способов:[9]

Вписанная окружность:

\ u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz-2wuzx-2uvxy=0

\pm {\sqrt {x}}\cos {\frac {A}{2}}\pm {\sqrt {y}}\cos {\frac {B}{2}}\pm {\sqrt {z}}\cos {\frac {C}{2}}=0

A-внешневписанная:

\ u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz+2wuzx+2uvxy=0

\pm {\sqrt {-x}}\cos {\frac {A}{2}}\pm {\sqrt {y}}\cos {\frac {B}{2}}\pm {\sqrt {z}}\cos {\frac {C}{2}}=0

B-внешневписанная:

\ u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz-2wuzx+2uvxy=0

\pm {\sqrt {x}}\cos {\frac {A}{2}}\pm {\sqrt {-y}}\cos {\frac {B}{2}}\pm {\sqrt {z}}\cos {\frac {C}{2}}=0

C-внешневписанная:

\ u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz+2wuzx-2uvxy=0

\pm {\sqrt {x}}\cos {\frac {A}{2}}\pm {\sqrt {y}}\cos {\frac {B}{2}}\pm {\sqrt {-z}}\cos {\frac {C}{2}}=0

Некоторые формулы с радиусом вписанной окружности

$r={\frac {p-a}{\operatorname {ctg} (\alpha /2)}}={\frac {p-b}{\operatorname {ctg} (\beta /2)}}={\frac {p-c}{\operatorname {ctg} (\gamma /2)}}$ , $p$ — полупериметр треугольника (Теорема котангенсов).

Радиус вписанной окружности не больше одной девятой суммы высот треугольника.[10]

Неравенство Эйлера: радиус вписанной окружности не превосходит половины радиуса описанной окружности и равенство имеет место лишь для равностороннего треугольника.[11]

Предположим, что точки касания вписанной окружности делят стороны на отрезки длиной x и y, y и z, z и x. Тогда вписанная окружность имеет радиус[12]

r={\sqrt {\frac {xyz}{x+y+z}}}

и площадь треугольника равна

K={\sqrt {xyz(x+y+z)}}.

Если высоты, опущенные на стороны a, b и c есть h_a, h_b и h_c, то радиус вписанной окружности r равен одной трети гармонического среднего этих высот, то есть

r={\frac {1}{h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1}}}.

Произведение радиуса вписанной окружности r и радиуса описанной окружности R треугольника со сторонами a, b и c равен[1]

rR={\frac {abc}{2(a+b+c)}}.

Некоторые связи сторон, радиусов вписанной окружности и описанной окружностей:[13]

ab+bc+ca=s^{2}+(4R+r)r,

a^{2}+b^{2}+c^{2}=2s^{2}-2(4R+r)r.

Любая прямая, проходящая через треугольник и делящая площадь треугольника и периметр пополам, проходит через центр вписанной окружности. Таких прямых может существовать три, две или одна.[14]

Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности [15].

Теорема Эйлера

Теорема Эйлера утверждает, что в треугольнике:[11]

(R-r_{in})^{2}=d^{2}+r_{in}^{2},

где R и r_in являются радиусами описанной и вписанной окружностей соответственно, а d — расстояние между центрами этих окружностей.

Для вневписанных окружностей уравнение выглядит похоже:

(R+r_{ex})^{2}=d^{2}+r_{ex}^{2},

где r_ex — радиус одной из вневписанных окружностей, а d — расстояние между центрами описанной и вневписанной окружностей. [16] [17] [18]

Возводя в квадрат и приводя подобные из первой формулы Эйлера выше имеем:

Квадрат расстояния от центра вписанной окружности I до центра описанной O задаётся уравнением[19]

OI^{2}=d^{2}=R(R-2r_{in}),

Аналогично для второй формулы:

d^{2}=R(R+2r_{ex}).

Другие формулы для расстояний до центра вписанной или вневписанной окружностей

Расстояние от центра вписанной окружности до центра N окружности девяти точек равно[19]

IN={\frac {1}{2}}(R-2r)<{\frac {1}{2}}R.

Расстояние от вершины до точек касания вписанной окружности на прилегающих сторонах равно полусумме длин прилегающих сторон минус половина противолежащей стороны.[20] Так, для вершины B и прилежащих точек касания T_A и T_C,

BT_{A}=BT_{C}={\frac {BC+AB-AC}{2}}.

Если обозначить центр вписанной окружности треугольника ABC буквой I, мы получим[21]

{\frac {IA\cdot IA}{CA\cdot AB}}+{\frac {IB\cdot IB}{AB\cdot BC}}+{\frac {IC\cdot IC}{BC\cdot CA}}=1

и[22]

IA\cdot IB\cdot IC=4Rr^{2}.

Если обозначить за I центр вписанной окружности треугольника ABC, AD — биссектриса угла A, то ${\frac {AI}{DI}}={\frac {AB+AC}{BC}}$
Центр вписанной окружности лежит в треугольнике, вершины которого являются серединами сторон треугольника.[19]
Теорема о трезубце или теорема трилистника, или теорема Клайнэра: Если D — точка пересечения биссектрисы угла A с описанной окружностью треугольника ABC, I и J — соответственно центры вписанной и вневписанной окружности, касающейся стороны BC, тогда $|DI|=|DB|=|DC|=|DJ|$ .

Теорема Мансиона (составная часть Теоремы о трезубце). Середины трёх отрезков, соединяющих центр вписанной окружности с центрами вневписанных окружностей лежат на описанной окружности.[11]

Теорема Харкорта

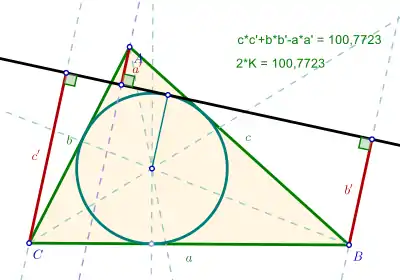
Теорема Харкорта. Пусть треугольник задан своими вершинами A, B и C, противоположные вершинам стороны имеют длины a, b и c, площадь равна K и прямая касается вписанной в треугольник окружности в произвольной точке. Обозначим расстояния от вершин треугольника до прямой через a ', b ' и c ', при этом, если вершина и центр окружности лежат по разные стороны от прямой, расстояние считается отрицательным. Тогда

aa^{\prime }+bb^{\prime }+cc^{\prime }=2K.

.

Другие свойства вневписанных окружностей

Следующее отношение выполняется для радиуса r вписанной окружности, радиуса R описанной окружности, полупериметра s и радиусов вневписанных окружностей r_a, r_b, r_c:[13]

r_{a}+r_{b}+r_{c}=4R+r,

r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}=s^{2},

r_{a}^{2}+r_{b}^{2}+r_{c}^{2}=(4R+r)^{2}-2s^{2},

Окружность, проходящая через центры вневписанных окружностей, имеет радиус 2R.[13]

Если H — ортоцентр треугольника ABC, то[13]

r_{a}+r_{b}+r_{c}+r=AH+BH+CH+2R,

r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}=AH^{2}+BH^{2}+CH^{2}+(2R)^{2}.

Вершины A, B и C треугольника ABC являются основаниями высот треугольника J_AJ_B,J_C,

где J_AJ_B,J_C — центры вневписанных окружностей. [11]

Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности [15].
Центр Шпикера треугольника является радикальным центром его вневписанных окружностей [23]. Если из центра Шпикера треугольника провести 6 касательных к 3 вневписанным окружностям треугольника, то все их длины будут равны между собой.

Определение окружности Аполлония

Точка Аполлония и окружность Аполлония

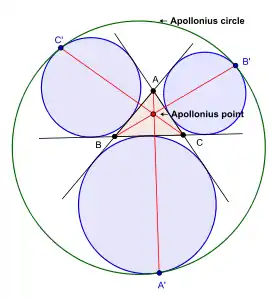
Пусть дан треугольник ABC. Пусть вневписанные окружности треугольника ABC, противоположные вершинам A, B и C, есть соответственно E_A, E_B, E_C (см. рисунок). Тогда окружность Аполлония E (на рис. справа показана зеленым цветом) касается внутренним образом сразу трех вневписанных окружностей треугольника ABC в точках соответственно E_A, E_B и E_C (см. рисунок).[24].

Радиус окружности Аполлония

Радиус окружности Аполлония равен ${\frac {r^{2}+s^{2}}{4r}}$ , где r — радиус вписанной окружности и s — полупериметр треугольника.[25]

Определение точки Аполлония Ap

Точка Аполлония Ap в Энциклопедии центров треугольника у Кларка Кимберлинга (Encyclopedia of Triangle Centers (ETC)) именуется как центр треугольника под именем X(181).
Точка Аполлония Ap или X(181) определяется следующим образом:

Пусть A' , B' и C' есть точки касания окружности Аполлония E с соответствтвующими вневписанными окружностями. Тогда прямые AA' , BB' и CC' пересекаются в одной точке Ap, которую называют точкой Аполлония треугольника ABC.

Изогональное сопряжение

Изогональное сопряжение имеет ровно четыре неподвижные точки (то есть точки, которые сопряжены самим себе): центр вписанной окружности и центры вневписанных окружностей треугольника.[26]

Ортоцентр треугольника изогонально сопряжён центру описанной окружности этого треугольника.[26]

Обобщение на другие многоугольники

Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
Некоторые (но не все) четырёхугольники имеют вневписанную окружность. Они называются внеописанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важное свойство отмечает теорема Уркхарта. Она утверждает:
Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F, то

AB+BC=AD+DC\quad \Leftrightarrow \quad AE+EC=AF+FC.

См. также

Примечания

Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007 (оригинал — 1929).. — С. 189, #298(d).
Стариков, 2016, с. 95-97.
H.S.M. Coxeter. Introduction to Geometry. — 2. — Wiley, 1961..
Marcus Baker. A collection of formulae for the area of a plane triangle. — January 1885. — Т. part 1, vol. 1(6). — С. 134-138.. См. также часть 2 в томе. 2(1), Сентябрь 1885, 11-18.)
D. Minda, S. Phelps. Triangles, ellipses, and cubic polynomials // American Mathematical Monthly. — October 2008. — Вып. 115. — С. 679-689: Theorem 4.1..
С. И. Зетель. Новая геометрия треугольника. — Москва: УЧПЕДГИЗ, 1962. — С. 52-53 Глава III.
Christopher J. Bradley, Geoff C. Smith. The locations of triangle centers // Forum Geometricorum. — 2006. — Вып. 6. — С. 57-70..
Deko Dekov. Computer-generated Mathematics : The Gergonne Point // Journal of Computer-generated Euclidean Geometry. — 2009. — Т. 1. — С. 1–14.. Архивировано 5 ноября 2010 года.
William Allen Whitworth. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions. — 2012. — С. 210-215. — (Forgotten Books).
Alfred S. Posamentier, Ingmar Lehmann. The Secrets of Triangles. — Prometheus Books, 2012. — С. 289.
А. Д. Куланин, С. Н. Федин. Геометрия треугольника в задачах. — М.: Книжный дом «ЛИБРОКОМ», 2009. — ISBN 978-5-397-00786-3.
Thomas Chu. The Pentagon. — Spring, 2005. — С. 45, задача 584..
Amy Bell. Hansen’s right triangle theorem, its converse and a generalization // Forum Geometricorum. — 2006. — Вып. 6. — С. 335–342.
Dimitrios Kodokostas. Triangle Equalizers // Mathematics Magazine. — 2010. — Вып. 83, April. — С. 141-146..
Мякишев, 2002, с. 11, п. 5.
Roger Nelson. Euler's triangle inequality via proof without words // Mathematics Magazine. — February 2008. — Вып. 81(1). — С. 58-61.
R. A. Johnson. Modern Geometry. — Boston: Houghton Mifflin, 1929. — С. 187.
Lev Emelyanov, Tatiana Emelyanova. Euler’s formula and Poncelet’s porism // Forum Geometricorum. — 2001. — Вып. 1. — С. 137–140..
William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. — 2011. — Т. 11. — С. 231–236..
Mathematical Gazette, July 2003, 323—324.
Patricia R. Allaire, Junmin Zhou, Haishen Yao. Proving a nineteenth century ellipse identity // Mathematical Gazette. — 2012. — Вып. 96, March. — С. 161-165..
Nathan Altshiller-Court. College Geometry. — Dover Publications, 1980. — С. 121,#84.
Odenhal, 2010, с. 35—40.
Darij Grinberg, Paul Yiu. The Apollonius Circle as a Tucker Circle // Forum Geometricorum. — 2002. — Вып. 2. — С. 175-182.
Milorad R. Stevanovi´c. The Apollonius circle and related triangle centers // Forum Geometricorum. — 2003. — Вып. 3. — С. 187-195..
В. В. Прасолов. Точки Брокара и изогональное сопряжение. — М.: МЦНПО, 2000. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-49-9.

Литература

Мякишев А.Г. Элементы геометрии треугольника. — М.: МЦНМО, 2002.
Стариков В.Н. По материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки». — Научный журнал Globus. — С-П., 2016.
Clark Kimberling. Triangle Centers and Central Triangles // Congressus Numerantium. — 1998. — Вып. 129. — С. i-xxv, 1-295.
Sándor Kiss. The Orthic-of-Intouch and Intouch-of-Orthic Triangles // Congressus Numerantium. — 2006. — Вып. 6. — С. 171—177.
Boris Odenhal. Some triangle centers associated with the circles tangent to the excircles // Forum Geometricorum. — 2010. — Т. 10.

Ссылки

Derivation of formula for radius of incircle of a triangle
Weisstein, Eric W. Incircle (англ.) на сайте Wolfram MathWorld.

Сайты с интерактивным содержанием

Triangle incenter Triangle incircle Incircle of a regular polygon With interactive animations
Constructing a triangle’s incenter / incircle with compass and straightedge An interactive animated demonstration
Equal Incircles Theorem at cut-the-knot
Five Incircles Theorem at cut-the-knot
Pairs of Incircles in a Quadrilateral at cut-the-knot
An interactive Java applet for the incenter

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Johnson-1] Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007 (оригинал — 1929).. — С. 189, #298(d).

[_33b7eb956a1fbfd8-2] Стариков, 2016, с. 95-97.

[3] H.S.M. Coxeter. Introduction to Geometry. — 2. — Wiley, 1961..

[4] Marcus Baker. A collection of formulae for the area of a plane triangle. — January 1885. — Т. part 1, vol. 1(6). — С. 134-138.. См. также часть 2 в томе. 2(1), Сентябрь 1885, 11-18.)

[5] D. Minda, S. Phelps. Triangles, ellipses, and cubic polynomials // American Mathematical Monthly. — October 2008. — Вып. 115. — С. 679-689: Theorem 4.1..

[6] С. И. Зетель. Новая геометрия треугольника. — Москва: УЧПЕДГИЗ, 1962. — С. 52-53 Глава III.

[Bradley-7] Christopher J. Bradley, Geoff C. Smith. The locations of triangle centers // Forum Geometricorum. — 2006. — Вып. 6. — С. 57-70..

[8] Deko Dekov. Computer-generated Mathematics : The Gergonne Point // Journal of Computer-generated Euclidean Geometry. — 2009. — Т. 1. — С. 1–14.. Архивировано 5 ноября 2010 года.

[WW-9] William Allen Whitworth. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions. — 2012. — С. 210-215. — (Forgotten Books).

[10] Alfred S. Posamentier, Ingmar Lehmann. The Secrets of Triangles. — Prometheus Books, 2012. — С. 289.

[Kulanin-11] А. Д. Куланин, С. Н. Федин. Геометрия треугольника в задачах. — М.: Книжный дом «ЛИБРОКОМ», 2009. — ISBN 978-5-397-00786-3.

[12] Thomas Chu. The Pentagon. — Spring, 2005. — С. 45, задача 584..

[Bell-13] Amy Bell. Hansen’s right triangle theorem, its converse and a generalization // Forum Geometricorum. — 2006. — Вып. 6. — С. 335–342.

[14] Dimitrios Kodokostas. Triangle Equalizers // Mathematics Magazine. — 2010. — Вып. 83, April. — С. 141-146..

[_9e92186e75a64935-15] Мякишев, 2002, с. 11, п. 5.

[Nelson-16] Roger Nelson. Euler's triangle inequality via proof without words // Mathematics Magazine. — February 2008. — Вып. 81(1). — С. 58-61.

[17] R. A. Johnson. Modern Geometry. — Boston: Houghton Mifflin, 1929. — С. 187.

[18] Lev Emelyanov, Tatiana Emelyanova. Euler’s formula and Poncelet’s porism // Forum Geometricorum. — 2001. — Вып. 1. — С. 137–140..

[Franzsen-19] William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. — 2011. — Т. 11. — С. 231–236..

[20] Mathematical Gazette, July 2003, 323—324.

[21] Patricia R. Allaire, Junmin Zhou, Haishen Yao. Proving a nineteenth century ellipse identity // Mathematical Gazette. — 2012. — Вып. 96, March. — С. 161-165..

[ac-22] Nathan Altshiller-Court. College Geometry. — Dover Publications, 1980. — С. 121,#84.

[_57af230a708b2e43-23] Odenhal, 2010, с. 35—40.

[24] Darij Grinberg, Paul Yiu. The Apollonius Circle as a Tucker Circle // Forum Geometricorum. — 2002. — Вып. 2. — С. 175-182.

[25] Milorad R. Stevanovi´c. The Apollonius circle and related triangle centers // Forum Geometricorum. — 2003. — Вып. 3. — С. 187-195..

[Prasolov-26] В. В. Прасолов. Точки Брокара и изогональное сопряжение. — М.: МЦНПО, 2000. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-49-9.