Степень точки относительно окружности

Степень точки относительно окружности — величина $d^{2}-R^{2}$ , где $d$ — расстояние от точки до центра окружности, a $R$ — радиус окружности. По этому определению точки внутри круга имеют отрицательные степени, точки вне круга имеют положительные степени, а точки на окружности имеют нулевую степень. Для точки, лежащей вне окружности, из теоремы Пифагора следует, что степень точки относительно окружности есть квадрат длины касательной, проведенных из данной точки к данной окружности. Степень точки также известна как степень окружности или степень круга относительно точки.

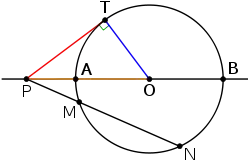
Степень внешней точки

P

относительно окружности равна

{\color {DarkOrange}PO}^{2}-{\color {blue}OT}^{2}=

{\color {red}PT}^{2}=

PA\cdot PB=

PM\cdot PN

Свойства

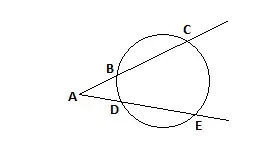
Теорема о двух секущих:

AB\cdot AC=AD\cdot AE

Если прямая, проходящая через точку $A$ $\text{[math]}$ , пересекает окружность $\Gamma$ $\text{[math]}$ в точках $B$ $\text{[math]}$ и $C$ $\text{[math]}$ , то степень $A$ $\text{[math]}$ относительно $\Gamma$ $\text{[math]}$ равна $\pm AB\cdot AC$ $\text{[math]}$ ; в этой формуле стоит «+» если $A$ $\text{[math]}$ лежит снаружи $\Gamma$ $\text{[math]}$ и «-» если внутри. В частности,
- (Теорема о двух секущих) Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть: $AB\cdot AC=AD\cdot AE$ (рис.).
- (Теорема о секущей и касательной) Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.

Связанные определения

Для двух не концентрических окружностей геометрическое место точек Р, для которых степени относительно обеих окружностей равны, является прямой, называемой радикальной осью окружностей.
Для трёх окружностей, центры которых не лежат на одной прямой существует единственная точка, такая, что её степени относительно всех трёх окружностей равны. Эта точка называется радикальным центром трёх окружностей.
Со степенью точки относительно окружности тесно связано понятие Инверсное расстояние.

История

Термин «степень» в этом значении был впервые употреблён Якобом Штейнером.

Вариации и обобщения

Аналогично определяется степень точки относительно сферы в $n$ -мерном евклидовом пространстве.

Литература

Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
Я. П. Понарин. §3.1 Степень точки относительно сферы // Элементарная геометрия. — М.: МЦНМО, 2006. — Т. 2. — С. 146. — 256 с. — 2000 экз. — ISBN 5-94057-223-5.

См. также

Ссылки

На Викискладе есть медиафайлы по теме Степень точки относительно окружности

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.