Теорема о произведении отрезков хорд

Теорема о произведении отрезков хорд описывает соотношения отрезков, образованных двумя пересекающимися хордами окружности. В теореме утверждается, что произведения длин отрезков каждой из хорд равны.

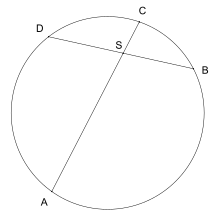
Формулировка теоремы

Для двух хорд AC и BD, пересекающихся в точке S, выполняется следующее равенство:

Обратное также верно, т. е. если для двух отрезков AC и BD, пересекающихся в точке S, вышеприведённое равенство выполняется, то их концы A, B, C и D лежат на одной окружности. Другими словами, если диагонали четырёхугольника ABCD пересекаются в точке S и выполняется вышеупомянутое равенство, то этот четырёхугольник является вписанным.

Степень точки

Значения двух произведений в теореме о хордах зависит от расстояния точки пересечения S от центра окружности и называется абсолютным значением степени точки S. Более точно это можно выразить следующим образом:

где r является радиусом окружности, а d является расстоянием между центром окружности и точкой пересечения S. Это свойство следует непосредственно из применения теоремы о хордах к третьей хорде, проведённой через точку S и центр окружности M (см. рисунок).

Наряду с теоремой о секущей и касательной и теоремой о двух секущих, теорема о пересекающихся хордах является одним из трёх основных случаев более общей теоремы о двух пересекающихся прямых и окружности — теоремы о степени точки.

Доказательство теоремы

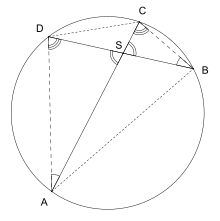
Теорему можно доказать с помощью подобных треугольников (через теорему о вписанном угле). Рассмотрим углы треугольников ASD и BSC:

(углы, опирающиеся на хорду AB)
(углы, опирающиеся на хорду CD)
(вертикальные углы)

Это означает, что треугольники ASD и BSC подобны, а потому:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «/mathoid/local/v1/»:): {\displaystyle \frac{AS}{SD}=\frac{BS}{SC} \Leftrightarrow |AS|\cdot|SC|=|BS|\cdot|SD|}

Вы можете посмотреть интерактивную иллюстрацию к теореме и её доказательству[1][2].

Примечания
  1. Amit Quackenbush. Intersecting Chords Theorem (англ.). GeoGebra. Дата обращения: 30 апреля 2021.
  2. Josiah Fan Ern Wei. Intersecting chord theorem (англ.). GeoGebra. Дата обращения: 30 апреля 2021.

Литература
  • Glaister P. Intersecting Chords Theorem: 30 Years on // Mathematics in School. — 2007. — vol. 36. — № 1. — P. 22.
  • Shawyer B. Explorations in Geometry. — World scientific, 2010. — P. 14. — ISBN 9789813100947.
  • Schupp H. Elementargeometrie. — Schöningh, Paderborn, 1977. — P. 149. — ISBN 3-506-99189-2.
  • Schülerduden — Mathematik I. — Bibliographisches Institut & F.A. Brockhaus, 2008. — S. 415—417. — ISBN 978-3-411-04208-1.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.