Барицентрические координаты

Пусть ${\displaystyle P}$ есть произвольная точка в ${\displaystyle A}$.  Каждая точка  ${\displaystyle M\in A}$  может быть единственным образом представлена в виде барицентрической комбинации

${\displaystyle M=P+\alpha _{0}\cdot {\overrightarrow {PP}}_{0}+\alpha _{1}\cdot {\overrightarrow {PP}}_{1}+\ldots +\alpha _{n}\cdot {\overrightarrow {PP}}_{n};}$

барицентричность стоящей в правой части линейной комбинации точек означает, что действительные числа ${\displaystyle \alpha _{0},\alpha _{1},\ldots ,\alpha _{n}}$ (коэффициенты комбинации) удовлетворяют условию

${\displaystyle \alpha _{0}+\alpha _{1}+\ldots +\alpha _{n}=1.}$

Барицентрические координаты (λ1,λ2,λ3) на равностороннем треугольнике и на прямоугольном треугольнике

Числа ${\displaystyle \alpha _{0},\alpha _{1},\ldots ,\alpha _{n}}$  и называются барицентрическими координатами точки ${\displaystyle M}$.  Легко видеть, что барицентрические координаты не зависят от выбора ${\displaystyle P}$.

Записанное выше равенство в символике барицентрического исчисления может быть переписано так:

${\displaystyle M=\alpha _{0}P_{0}+\alpha _{1}P_{1}+\ldots +\alpha _{n}P_{n}.}$

• Барицентрические координаты аффинно инвариантны.
• Барицентрические координаты точек симплекса с вершинами в ${\displaystyle P_{0},P_{1},\ldots ,P_{n}}$ неотрицательны и их сумма равна единице.
• Обращение в нуль барицентрической координаты ${\displaystyle \alpha _{i}}$ равносильно тому, что точка лежит на плоскости, содержащей грань симплекса, противоположную вершине ${\displaystyle P_{i}}$. Это свойство позволяет рассматривать барицентрические координаты точек симплициального комплекса относительно всех его вершин.
• В барицентрических координатах изотомическое сопряжение двух точек внутри треугольника задаётся формулой ${\displaystyle (x:y:z)\mapsto (x^{-1}:y^{-1}:z^{-1})}$. В связи с этим, барицентрические координаты часто бывают удобны при работе с изотомическим сопряжением.
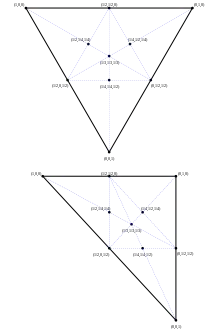
• Для точки ${\displaystyle X}$, лежащей внутри треугольника ${\displaystyle ABC}$, в качестве барицентрических координат можно взять площади треугольников ${\displaystyle (S_{BCX}:S_{CAX}:S_{ABX})}$.
• Барицентрические координаты тесно связаны с трилинейными координатами. А именно, если ${\displaystyle (\alpha$ :\beta :\gamma )}  — барицентрические координаты точки ${\displaystyle X}$ относительно треугольника ${\displaystyle ABC}$, а ${\displaystyle a,b,c}$ — длины его сторон, то

  ${\displaystyle (x:y:z)=\left({\frac {\alpha }{a}}:{\frac {\beta }{b}}:{\frac {\gamma }{c}}\right)}$

её трилинейные координаты. Трилинейные координаты, как и барицентрические, определены с точностью до пропорциональности.

• Точка ${\displaystyle M}$ является центром масс грузиков с массами ${\displaystyle \alpha _{0},\alpha _{1},\ldots ,\alpha _{n}}$, расположенных в точках ${\displaystyle P_{0},P_{1},\ldots ,P_{n}}$.

Барицентрические координаты введены Мёбиусом в 1827 г.[2]

• Балк М. Б., Болтянский В. Г.  Геометрия масс. — М.: Наука, 1987. — 160 с. — (Библиотечка «Квант». Вып. 61).
• Кострикин А. И., Манин Ю. И.  Линейная алгебра и геометрия. — М.: Наука, 1986. — 304 с.
• Боголюбов А. Н.  Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.

• Трилинейные координаты
• Аффинные преобразования
• Аффинное пространство