Единичная окружность

Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.

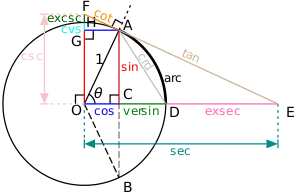
С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).

Синус и косинус могут быть описаны следующим образом: если соединить любую точку ${\displaystyle (x,y)}$ на единичной окружности с началом координат ${\displaystyle (0,0)}$, получается отрезок, находящийся под углом ${\displaystyle \alpha }$ относительно положительной полуоси абсцисс. Тогда действительно:

${\displaystyle \cos \alpha =x}$,

${\displaystyle \sin \alpha =y}$.

При подстановке этих значений в уравнение окружности ${\displaystyle x^{2}+y^{2}=1}$ получается:

${\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1}$.

(Используется следующая общепринятая нотация: ${\displaystyle \cos ^{2}x=(\cos x)^{2}}$.)

Тут же наглядно описывается периодичность тригонометрических функций, так как соответствующее углу положение отрезка не зависит от количества «полных оборотов»:

${\displaystyle \sin(x+2\pi k)=\sin(x)}$

${\displaystyle \cos(x+2\pi k)=\cos(x)}$

для всех целых чисел ${\displaystyle k}$, то есть для ${\displaystyle k\in \mathbb {Z} }$.

В комплексной плоскости единичная окружность — это следующее множество ${\displaystyle G\subset \mathbb {C} }$:

${\displaystyle G=\{z:\mathrm {Re} \{z\}^{2}+\mathrm {Im} \{z\}^{2}=1\}=\{z:z=e^{i\phi },0\leq \phi <2\pi \}}$

Множество ${\displaystyle G}$ является подгруппой группы комплексных чисел по умножению, её нейтральный элемент — это ${\displaystyle e^{i0}=1}$).

• Единичная сфера
• Единичный квадрат
• Единичный куб