Тригонометрическая подстановка
В математике тригонометрическая подстановка — это подстановка из тригонометрических функций для других выражений. В исчислении тригонометрическая подстановка — это метод вычисления интегралов. Более того, можно использовать тригонометрические тождества для упрощения некоторых интегралов, содержащих радикальное выражение[1][2]. Как и другие методы интегрирования путём подстановки, при вычислении определённого интеграла может быть проще полностью вывести первообразную перед применением границ интегрирования.
Случай I: Подынтегральные выражения, содержащие a2 − x2
Пусть , и используйте тождество .
Примеры Случая I

Пример 1
В интеграле
можно использовать
Тогда
Вышеупомянутый шаг требует, чтобы и . Мы можем выбрать в качестве главного корня и наложить ограничение с помощью функции обратного синуса.
Для определённого интеграла нужно выяснить, как меняются границы интегрирования. Например, если изменяется от до , тогда изменяется от до , поэтому изменяется от до . Тогда
При выборе границ требуется некоторая осторожность. Поскольку приведённая выше интеграция требует, чтобы , значение может изменяться только от до . Пренебрегая этим ограничением, можно было бы выбрать для перехода от к , что привело бы фактически к отрицательному значению.
В качестве альтернативы можно полностью вычислить неопределённые интегралы перед применением граничных условий. В этом случае первообразная даёт
как прежде.
Пример 2
Интеграл
можно оценить путём представления
где , так что и по диапазону арксинуса, так что и .
Тогда
Для определённого интеграла границы изменяются после выполнения замены и определяются с помощью уравнения со значениями в диапазоне . Или же можно применить граничные члены непосредственно к формуле первообразной.
Например, определённый интеграл
можно оценить, подставив , с оценками, определёнными с помощью , и .
Тогда
С другой стороны, прямое применение граничных членов к ранее полученной формуле для первообразных даёт
как прежде.
Случай II: Подынтегральные выражения, содержащие a2 + x2
Примеры Случая II

Пример 1
В интеграле
можно написать
так что интеграл становится
при условии .
Для определённого интеграла границы изменяются после выполнения замены и определяются с помощью уравнения со значениями в диапазоне . Или же можно применить граничные члены непосредственно к формуле первообразной.
Например, определённый интеграл
можно оценить, подставив , с оценками, определёнными с помощью , и .
Тогда
Между тем, прямое применение граничных членов к формуле для первообразных даёт
так же, как прежде.
Пример 2
Интеграл
можно оценить путём представления
где , так что и по диапазону арктангенса, так что и .
Тогда
Интеграл секанса в кубе можно вычислить с помощью интегрирования по частям. Как результат
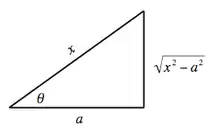
Случай III: Подынтегральные выражения, содержащие x2 − a2
Пусть и используется тождество
Примеры Случая III
Интегралы типа
также можно вычислить частичными дробями, а не тригонометрическими подстановками. Однако интеграл
нельзя. В этом случае подходящей подстановкой будет:
где , так что и , предполагая , так что и .
Тогда
Можно вычислить интеграл функции секанс, умножив числитель и знаменатель на и интеграл секанса в кубе по частям[3]. Как результат
Если , что происходит, когда с заданным диапазоном арксеканса, то , что в данном случае означает .
Подстановки, исключающие тригонометрические функции
Подстановка может использоваться для удаления тригонометрических функций.
Например,
Последняя подстановка известна как подстановка Вейерштрасса, в которой используются формулы тангенса половинного угла.
Например,
Гиперболическая подстановка
Подстановки гиперболических функций также могут использоваться для упрощения интегралов[4].
В интеграле можно сделать подстановку ,
Затем, используя тождества и
можно получить
Примечания
- Джеймс Стюарт. Исчисление: ранние трансцендентальные теории. — 6-е издание. — Брукс/Коул, 2008. — ISBN 978-0-495-01166-8.
- Джордж Б. Томас, Морис Д. Вейр, Джоэл Хасс. Исчисление Томаса: ранние трансценденталы. — 12-е издание. — Addison-Wesley, 2010. — ISBN 978-0-321-58876-0.
- Джеймс Стюарт. Раздел 7.2: Тригонометрические интегралы // Исчисление — Ранние трансцендентальные теории. — Соединенные Штаты : Cengage Learning, 2012. — P. 475–6. — ISBN 978-0-538-49790-9.
- Христо Н. Бояджиев. Гиперболические подстановки интегралов. Дата обращения: 4 марта 2013.