Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка, в англоязычной литературе называемая в честь Карла Вейерштрасса подстановкой Вейерштрасса, применяется в интегрировании для нахождения первообразных, определённых и неопределённых интегралов от рациональных функций от тригонометрических функций. Без потери общности можно считать в данном случае такие функции рациональными функциями от синуса и косинуса. Подстановка использует тангенс половинного угла.
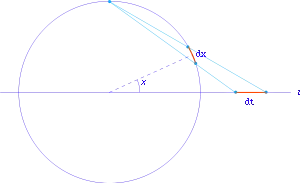
Подстановка
Рассмотрим задачу нахождения первообразной рациональной функции от синуса и косинуса.
Заменим sin x, cos x и дифференциал dx рациональными функциями от переменной t, и их произведением дифференциал dt, следующим образом:[1]
для значений x, лежащих в интервале
Введение обозначений
Примем, что переменная t равна тангенсу половинного угла:
В интервале −π < x < π, это даёт
и после дифференцирования получаем
Формула тангенса половинного угла даёт для синуса
и для косинуса формула даёт
Примеры
Первый пример
Найдём интеграл
Используя подстановку Вейерштрасса, получаем
Чтобы вычислить последний интеграл, используем разложение дробей:
Далее, согласно формуле тангенса половинного угла, можно заменить tg(x/2) на sin x/(1 + cos x), и тогда получаем
или так же мы можем заменить tg(x/2) на (1 − cos x)/sin x.
Второй пример: определённый интеграл
Разница между определённым и неопределённым интегрированием состоит в том, что при вычислении определённого интеграла нам не обязательно преобразовывать полученную функцию от переменной t обратно к функции от переменной x, если корректно изменить пределы интегрирования.
Например,
Если x изменяется от 0 до π/6, sin x изменяется от 0 до 1/2. Это означает, что величина 2t/(1 + t2), равная sin изменяется от 0 до 1/2. Тогда можно найти пределы интегрирования по переменной t:
перемножая обе части уравнения на 2 и на (1 + t2), получаем:
Решая квадратное уравнение, получаем два корня
Возникает вопрос: какой из этих двух корней подходит для нашего случая? Ответить на него можно, рассмотрев поведение
как функцию от x и как функцию от t. Когда x изменяется 0 до π, функция sin x изменяется от 0 до 1, и потом назад до 0. Эта функция проходит через значение 1/2 дважды — при изменении от 0 до 1 и при обратном изменении от 1 до 0. Когда t изменяется от 0 до ∞, функция 2t/(1 + t2) изменяется от 0 до 1 (когда t = 1) и потом обратно до to 0. Она проходит значение 1/2 при изменении от 0 до 1 и при обратном изменении: первый раз при t = 2 − √3 и потом опять при t = 2 + √3.
Произведя несложные алгебраические преобразования, получим
Выделяя полный квадрат, получаем
Введём новую переменную
Отсюда
при
и предел интегрирования будет
так как выше было определено, что
Тогда интегрирование даёт
На последнем шаге использовано известное тригонометрическое тождество
Третий пример
Подстановку Вейерштрасса можно использовать при нахождении интеграла от секанса:
Имеем
Как и в первом примере, используем разложение дроби:
Геометрия
Линейное преобразование дробей
Два компонента
являются соответственно действительной и мнимой частями числа
(считаем, что t действительное).
Примечания
- James Stewart, Calculus: Early Transcendentals, Brooks/Cole, 1991, page 439
Ссылки
- Подстановка Вейерштрасса на сайте PlanetMath
- Weisstein, Eric W. "Weierstrass Substitution." From MathWorld—A Wolfram Web Resource. (англ.)