Корень (математика)
Корень -й степени из числа определяется[1] как такое число , что Здесь — натуральное число, называемое показателем корня (или степенью корня); как правило, оно больше или равно 2, потому что случай не представляет интереса.
- Это статья об извлечении корней. См. также Корень уравнения и Корень многочлена.
 |
Обозначение: символ (знак корня) в правой части называется радикалом. Число (подкоренное выражение) чаще всего вещественное или комплексное, но существуют и обобщения для других математических объектов, например, вычетов, матриц и операторов, см. ниже #Вариации и обобщения.
Примеры для вещественных чисел:
- Корнями 2-й степени из числа 9 являются и у обоих этих чисел квадраты совпадают и равны 9
- потому что
- потому что
Как видно из первого примера, у вещественного корня чётной степени могут быть два значения (положительное и отрицательное), и это затрудняет работу с такими корнями, не позволяя использовать их в арифметических вычислениях. Чтобы обеспечить однозначность, вводится понятие арифметического корня (из неотрицательного вещественного числа), значение которого всегда неотрицательно, в первом примере это число Кроме того, принято соглашение, по которому знак корня чётной степени из вещественного числа всегда обозначает арифметический корень[2][3]: Если требуется учесть двузначность корня, перед радикалом ставится знак плюс-минус[2]; например, так делается в формуле решения квадратного уравнения :
Вещественные корни чётной степени из отрицательных чисел не существуют. Из комплексного числа всегда можно извлечь корень любой степени, но результат определён неоднозначно — комплексный корень -й степени из ненулевого числа имеет различных значений (см. #Корни из комплексных чисел).
Операция извлечения корня и алгоритмы её реализации появились в глубокой древности в связи с практическими потребностями геометрии и астрономии, см. #История.
Определение и связанные понятия
Кроме приведенного выше, можно дать два равносильных определения корня[4]:
- Корень -й степени из числа есть решение уравнения (отметим, что решений может быть несколько или ни одного)
- Корень -й степени из числа есть корень многочлена то есть значение , при котором указанный многочлен равен нулю.
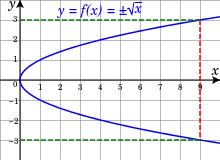
Операция вычисления называется «извлечением корня -й степени» из числа . Это одна из двух операций, обратных по отношению к возведению в степень[5], а именно — нахождение основания степени по известному показателю и результату возведения в степень . Вторая обратная операция, логарифмирование, находит показатель степени по известным основанию и результату.
Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия[5].
- Квадратный корень: В этом случае показатель степени 2 обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Геометрически можно истолковать как длину стороны квадрата, площадь которого равна .
- Кубический корень: Геометрически — это длина ребра куба, объём которого равен .
Корни из вещественных чисел
В данном разделе всюду — натуральное число, — вещественные числа. Корень -й степени из вещественного числа , в зависимости от чётности и знака , может иметь от 0 до 2 вещественных значений.
Общие свойства
- Корень нечётной степени из положительного числа — положительное число, однозначно определенное.
| , где — нечётное |
- Например,
- Корень нечётной степени из отрицательного числа — отрицательное число, однозначно определенное.
| , где — нечётное |
- Например,
- Корень чётной степени из положительного числа имеет два значения с противоположными знаками, но равными по модулю.
| , где — чётное |
- Например,
- Корень чётной степени из отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число. Ниже будет показано, как извлекать такие корни в более широкой системе — множестве комплексных чисел (тогда значениями корня будут комплексных чисел).
| не существует в области вещественных чисел, если — чётное |
- Корень любой натуральной степени из нуля — ноль.
Предостережение
Как сказано выше: «Корень чётной степени из отрицательного числа не существует в области вещественных чисел». При этом в области комплексных чисел такой корень существует. Поэтому следует всегда учитывать, в какой числовой системе (вещественных или комплексных чисел) мы извлекаем корень.
- Пример. В области вещественных чисел, квадратный корень из не существует.
- Пример. В области комплексных чисел, квадратный корень из равен
Арифметический корень

Выше уже говорилось, что корни чётной степени определены, вообще говоря, неоднозначно, и этот факт создаёт неудобства при их использовании. Поэтому было введено практически важное ограничение этого понятия[6].
Арифметический корень -й степени из неотрицательного вещественного числа — это неотрицательное число , для которого Обозначается арифметический корень знаком радикала.
Таким образом, арифметический корень, в отличие от корня общего вида (алгебраического), определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно[7] и неотрицательно. Например, квадратный корень из числа имеет два значения: и , из них арифметическим является первое.
Алгебраические свойства
Приведённые ниже формулы верны, прежде всего, для арифметических корней любой степени (кроме особо оговоренных случаев). Они справедливы также для корней нечётной степени, у которых допускаются и отрицательные подкоренные выражения[8].
- Взаимопогашение корня и степени:[9]
- для нечётного : ,
- для чётного :
- Если , то и
Корень из произведения равен произведению корней из сомножителей:
Аналогично для деления:
Следующее равенство есть определение возведения в дробную степень[10]:
Величина корня не изменится, если его показатель и степень подкоренного выражения разделить на одно и то же число (множитель показателя степени и показатель степени подкоренного выражения):
- Пример:
Для корней нечётной степени укажем дополнительное свойство:
Извлечение корня и возведение в дробную степень
Операция возведения в степень первоначально была введена как сокращённая запись операции умножения натуральных чисел: . Следующим шагом было определение возведения в произвольную целую, в том числе отрицательную, степень:
Операция извлечения арифметического корня позволяет определить возведение положительного числа в любую рациональную (дробную) степень[10]:
При этом числитель дроби может иметь знак. Свойства расширенной операции в основном аналогичны возведению в целую степень.
Это определение означает, что извлечение корня и обратное к нему возведение в степень фактически объединяются в одну алгебраическую операцию. В частности:
Попытки возведения в рациональную степень отрицательных чисел могут привести к ошибкам, поскольку значение алгебраического корня неоднозначно, а область значений арифметического корня ограничена неотрицательными числами. Пример возможной ошибки:
Функция корня
- Графики функций корня
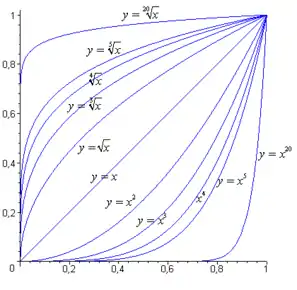 Функции корня и обратные к ним степенные функции на интервале
Функции корня и обратные к ним степенные функции на интервале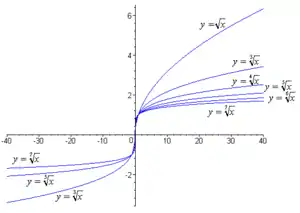 Функции корня:
Функции корня:
— арифметический, чётные степени 2, 4, 6
— общий, нечётные степени 3, 5, 7
Если рассматривать подкоренное выражение как переменную, мы получим функцию корня -й степени: . Функция корня относится к категории алгебраических функций. График любой функции корня проходит через начало координат и точку .
Как сказано выше, для корня чётной степени, чтобы обеспечить однозначность функции, корень должен быть арифметическим, так что аргумент неотрицателен. Функция корня нечётной степени однозначна и существует для любого вещественного значения аргумента.
| Тип функции корня | Область определения | Область значений | Другие свойства |
|---|---|---|---|
| Чётной степени | Функция выпукла вверх на всей области определения | ||
| Нечётной степени | Функция нечётна |
Для любой степени функция корня строго возрастает, непрерывна всюду внутри своей области определения. Неограниченно дифференцируема всюду, кроме начала координат, где производная обращается в бесконечность[11] [12]. Производная определяется по формуле[13]:
- . В частности, .
Функция неограниченно интегрируема во всей области определения. Неопределенный интеграл ищется по формуле:
- . В частности, , где — произвольная постоянная.
- Формула нахождения производной -го порядка[14] функции :
| где |
- Формула нахождения -го неопределённого интеграла[15] функции :
| где |
- Правые части формул являются алгебраическими выражениями, которые существуют всегда, при натуральном . Следовательно и левые тоже.
Практическое вычисление корней
Функция вычисления квадратных и кубических корней предусмотрена во многих калькуляторах; например, калькулятор Windows показывает соответствующие кнопки в режиме «Инженерный» (Научный). Если на электронном калькуляторе есть клавиша возведения в степень: то для извлечения корня из текущего числа надо нажать следующие клавиши[17].
- Набрать показатель корня
- Нажать клавишу
- Нажать клавишу
Для расчёта вручную можно использовать быстро сходящийся метод, изложенный в статье «Алгоритм нахождения корня n-ной степени». Для степеней выше третьей можно использовать логарифмическое тождество:
Для извлечения корня надо найти логарифм подкоренного выражения, разделить на степень корня и найти антилогарифм результата.
Корни из комплексных чисел
Зарождение понятия комплексного числа исторически было связано с желанием «легализовать» квадратные корни из отрицательных чисел. Как постепенно выяснилось, комплексные числа обладают богатыми алгебраическими и аналитическими свойствами; в частности, извлечение корней из них всегда возможно, хотя и неоднозначно. Для корней в комплексной области знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней; в последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Пример возможной ошибки:
- (что, конечно, неверно)
Ошибка возникла из-за того, что неарифметический квадратный корень является многозначной функцией, и его нельзя использовать в арифметических действиях.
Способы нахождения
Запишем комплексное число в тригонометрической форме:
- .
Тогда корни -й степени из определяются формулой Муавра (тригонометрическая форма)[18]:
или в показательной форме:
Обозначения (комплексное число), |
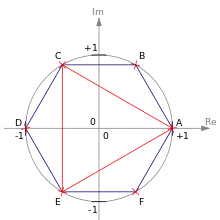
Корень степени из ненулевого комплексного числа имеет значений (это следствие основной теоремы алгебры), и все они различны. Значение корня, получаемое при , часто называется главным.
Поскольку для всех значений корня величина модуля одинакова (он определяется как арифметический корень из модуля изначального комплексного числа), а меняется лишь его аргумент, все значений корня располагаются на комплексной плоскости на окружности радиуса c центром в начале координат. Корни делят эту окружность на равных частей.
Примеры
Найдём . Поскольку по формуле получаем:
При получим первый корень , при получим второй корень
Другой пример: найдём . Представим подкоренное выражение в тригонометрической форме:
По формуле Муавра получаем:
В итоге имеем четыре значения корня[19]:
Можно записать сводный ответ в виде:
Комплексная функция корня и риманова поверхность
Рассмотрим комплексную функцию корня -й степени: Согласно сказанному выше, эта функция является многозначной (точнее, -значной) функцией, и это создаёт неудобства при её исследовании и применении. В комплексном анализе вместо рассмотрения многозначных функций на комплексной плоскости принято иное решение: рассматривать функцию как однозначную, но определённую не на плоскости, а на более сложном многообразии, которое называется римановой поверхностью[20].
 Риманова поверхность для комплексного квадратного корня
Риманова поверхность для комплексного квадратного корня Риманова поверхность для комплексного корня 4-й степени
Риманова поверхность для комплексного корня 4-й степени
Для комплексной функции корня -й степени её риманова поверхность (см. рисунки) состоит из ветвей (листов), связанных винтообразно, причём последний лист связан с первым. Эта поверхность непрерывна и односвязна. Один из листов содержит главные значения корня, получаемые как аналитическое продолжение вещественного корня с положительного луча вещественной оси.
Опишем для простоты комплексную функцию квадратного корня. Её риманова поверхность состоит из двух листов. Первый лист можно представить как комплексную плоскость, у которой вырезан положительный луч вещественной оси. Значения функции корня на этом листе имеют вдвое меньший аргумент, чем , и поэтому они заполняют верхнюю часть комплексной плоскости значений. На разрезе первый лист склеен со вторым, и функция непрерывно продолжается через разрез на второй лист, где её значения заполняют нижнюю часть комплексной плоскости значений. Оставшиеся свободными начало первого листа и конец второго тоже склеим, после чего полученная функция на римановой поверхности становится однозначной и всюду непрерывной[20].
Единственный нуль у функции (первого порядка) получается при . Особые точки: и (точки разветвления бесконечного порядка)[20]. Понятие точки разветвления означает, что замкнутый контур в окрестности нуля неизбежно содержит переход с листа на лист.
В силу односвязности риманова поверхность корня является универсальной накрывающей[21] для комплексной плоскости без точки .
Вариации и обобщения
Корень -й степени из есть решение уравнения , и его в принципе можно определить всюду, где такое уравнение имеет смысл. Чаще всего рассматривают такие обобщения в алгебраических кольцах. Лучше всего исследованы обобщённые квадратные корни.
Если кольцо есть область целостности, то квадратных корней из ненулевого элемента может быть либо два, либо ни одного. В самом деле, если имеются два корня то откуда: , то есть, в силу отсутствия делителей нуля, . В более общем случае, когда в кольце имеются делители нуля или оно некоммутативно, число корней может быть любым.
В теории чисел рассматривается конечное кольцо вычетов по модулю : если сравнение имеет решение, то целое число называется вычетом степени n (в противном случае — невычетом степени n). Решение , если оно существует, является полным аналогом корня n-й степени из целого числа . Чаще всего используются случаи[22]:
- (квадратичные вычеты)
- (кубические вычеты)
- (биквадратичные вычеты)
Корни для кватернионов имеют много общего с комплексными, но есть и существенные особенности. Квадратный кватернионный корень обычно имеет 2 значения, но если подкоренное выражение — отрицательное вещественное число, то значений бесконечно много. Например, квадратные корни из образуют трёхмерную сферу, определяемую формулой[23]:
Для кольца квадратных матриц доказано, что если матрица положительно определена, то положительно определённый квадратный корень из матрицы существует и единственен[24]. Для матриц других типов корней может быть сколько угодно (в том числе ни одного).
Квадратные корни вводятся также для функций[25], операторов[26] и других математических объектов.
История
Развитие понятия

Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков (о достижениях древнего Египта в этом отношении ничего не известно). Среди таких задач[27]:
- Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.
- Нахождение стороны квадрата, площадь которого задана.
- Решение квадратных уравнений.
Вавилонские математики (II тысячелетие до н. э.) разработали для извлечения квадратного корня особый численный метод. Начальное приближение для рассчитывалось исходя из ближайшего к корню (в меньшую сторону) натурального числа . Представив подкоренное выражение в виде: , получаем: , затем применялся итеративный процесс уточнения, соответствующий методу Ньютона[28]:
Итерации в этом методе очень быстро сходятся. Для , например, и мы получаем последовательность приближений:
В заключительном значении верны все цифры, кроме последней.
Аналогичные задачи и методы встречаются в древнекитайской «Математике в девяти книгах»[29]. Древние греки сделали важное открытие: — иррациональное число. Детальное исследование, выполненное Теэтетом Афинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально[30].
Греки сформулировали проблему удвоения куба, которая сводилась к построению кубического корня с помощью циркуля и линейки. Проблема оказалась неразрешимой. Численные алгоритмы извлечения кубического корня опубликовали Герон (в трактате «Метрика», I век н. э.) и индийский математик Ариабхата I (V век)[31].
Алгоритмы извлечения корней любой степени из целого числа, разработанные индийскими и исламскими математиками, были усовершенствованы в средневековой Европе. Николай Орем (XIV век) впервые истолковал[32] корень -й степени как возведение в степень .
После появления формулы Кардано (XVI век) началось применение в математике мнимых чисел, понимаемых как квадратные корни из отрицательных чисел[33]. Основы техники работы с комплексными числами разработал в XVI веке Рафаэль Бомбелли, который также предложил оригинальный метод вычисления корней (с помощью цепных дробей). Открытие формулы Муавра (1707) показало, что извлечение корня любой степени из комплексного числа всегда возможно и не приводит к новому типу чисел[34].
Комплексные корни произвольной степени в начале XIX века глубоко исследовал Гаусс, хотя первые результаты принадлежат Эйлеру[35]. Чрезвычайно важным открытием (Галуа) стало доказательство того факта, что не все алгебраические числа (корни многочленов) могут быть получены из натуральных с помощью четырёх действий арифметики и извлечения корня[36].
Этимология термина и происхождение символики
Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически: как нахождение стороны квадрата по известной его площади. После перевода на санскрит греческое слово «сторона» превратилась в «мула» (основание). Слово «мула» имело также значение «корень», поэтому при переводе индийских сиддхант на арабский использовался термин «джизр» (корень растения). Впоследствии аналогичное по смыслу слово «radix» закрепилось в латинских переводах с арабского, а через них и в русской математической терминологии («корень», «радикал»)[37].
Средневековые математики (например, Кардано) обозначали квадратный корень[38] символом Rx, сокращение от слова «radix». Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов (то есть алгебраистов), в 1525 году[39]. Происходит этот символ от стилизованной первой буквы того же слова «radix». Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт (1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.
Показатель степени появился в знаке корня благодаря Валлису и «Универсальной арифметике» Ньютона (XVIII век)[40].
См. также
Литература
- Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М.: Наука, 1970—1972.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
- Мордкович А. Г. Алгебра и начала анализа. Учебник для 10—11 классов, часть 1. — изд. 4-е. — М.: Мнемозина, 2003. — 376 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
Примечания
- Корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- Элементарная математика, 1976, с. 49.
- Корн Г., Корн Т. Справочник по математике, 1970, с. 33.
- Сканави М. И. Элементарная математика. П. 1.11. С. 49.
- Выгодский М. Я. Справочник по элементарной математике, 1978, с. 64.
- Арифметический корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 35—36.
- Выгодский М. Я. Справочник по элементарной математике, 1978, с. 141—143.
- Алгебра и начала анализа. Учебник для 10—11 классов, под ред. А. Н. Колмогорова. М.: Просвещение, 2002, С. 209.
- Выгодский М. Я. Справочник по элементарной математике, 1978, с. 183.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 194, 198.
- Мордкович А. Г., 2003, с. 236—238.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 215.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Т. I, С. 233, частный случай для .
- Не путать с кратными интегралами. Их записи весьма похожи, но -й интеграл является неопределённым, в то время как -кратный интеграл — определённый.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 67, 131—132, 164, 166—167.
- Алгебра. 9 класс. Учебник для общеобразовательных учреждений / Под ред. С. А. Теляковского. — Изд. 18-е. — М.: Просвещение, 2011. — С. 53. — ISBN 978-5-09-025168-6.
- Корн Г., Корн Т. Справочник по математике, 1970, с. 36—37.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — издание третье, стереотипное. — М.: Наука, 1976. — С. 68. — 591 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 96-99, 28—29.
- Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).
- Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — С. 71. — 180 с.
- Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
- См., например: Гантмахер Ф. Р. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, или: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
- См., например: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, или: Каплан И. А. Практические занятия по высшей математике. Харьков: Изд-во ХГУ, 1966.
- См., например: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, или: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.
- История математики, 1970—1972, Том I, С. 42—46.
- История математики, 1970—1972, Том I, С. 47.
- История математики, 1970—1972, Том I, С. 169—171.
- Башмакова И. Г. Становление алгебры (из истории математических идей). — М.: Знание, 1979. — С. 23. — (Новое в жизни, науке, технике. Математика, кибернетика, № 9).
- Abhishek Parakh. Ariabhata's root extraction methods // Indian Journal of History of Science. — 2007. — Вып. 42.2. — С. 149—161. Архивировано 9 июня 2010 года.
- История математики, 1970—1972, Том I, С. 275—276.
- История математики, 1970—1972, Том I, С. 296—298.
- История математики, 1970—1972, Том III, С. 56—59.
- История математики, 1970—1972, Том III, С. 62.
- Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I. — С. 58—66.
- История математики, 1970—1972, Том I, С. 185.
- Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 81. — 208 с. — (История науки и техники).
- Знаки математические // Математическая энциклопедия. — М.: Советская Энциклопедия, 1982. — Т. 2.
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб.: ЛКИ, 2008. — С. 82. — 248 с. — ISBN 978-5-382-00839-4.
