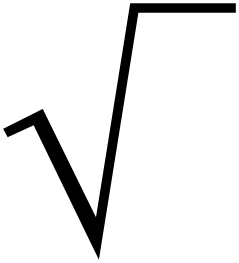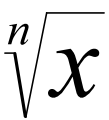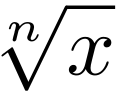Знак корня

Знак корня (знак радикала) (√) в математике — условное обозначение для корней, по умолчанию квадратных. В общем случае (для корней n-й степени) показатель степени ставится над «птичкой»: знак используется для кубических корней,  — для корней 4-й степени и т. п.; для квадратного корня также можно использовать «полное» обозначение .

Знак корня
√∛∜
Изображение
◄ ∖ ∗ ∘ ∙ √ ∛ ∜ ∝ ∞ ►
◄ ∗ ∘ ∙ √ ∛ ∜ ∝ ∞ ∟ ►
◄ ∘ ∙ √ ∛ ∜ ∝ ∞ ∟ ∠ ►
Характеристики
Название √: square root
∛: cube root
∜: fourth root
Юникод √: U+221A
∛: U+221B
∜: U+221C
HTML-код √‎: √ или √
∛‎: ∛ или ∛
∜‎: ∜ или ∜
UTF-16 √‎: 0x221A
∛‎: 0x221B
∜‎: 0x221C
URL-код √: %E2%88%9A
∛: %E2%88%9B
∜: %E2%88%9C
Мнемоника √: √

Корни чётной степени из вещественных чисел неоднозначны — например, у числа 9 существуют два квадратных корня, и Во избежание недоразумений принято соглашение, что под знаком корня чётной степени из вещественного числа может находиться только неотрицательное число (см. Арифметический корень)[1][2]. Для корней в комплексной области знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней; в последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях (см. Комплексные корни).

История

Знак корня происходит из строчной латинской буквы r (начальной в лат. radix — корень), сросшейся с надстрочной чертой: ранее надчёркивание выражения использовалось вместо нынешнего заключения его в скобки. Так что есть всего лишь видоизменённый способ записи выражения .

Впервые такое обозначение использовал немецкий математик Кристоф Рудольф в 1525 году. Им также были изобретены символы и для корней третьей и четвёртой степеней соответственно, однако они не закрепились в науке[3].

Типографика
  • американский вариант
  • немецкий вариант
  • русский вариант [4]
  • вариант TeX

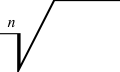
В некоторых типографских традициях (например, в германской) принято верхнюю черту знака корня снабжать справа небольшой обращённой вниз засечкой. В Американской типографике (в частности, системе TEΧ) этой детали нет.

Длина и высота знака корня должны быть такими, чтобы полностью покрывать подкоренное выражение. При соседстве в одной строке нескольких подкоренных выражений разной (но близкой) высоты часто бывает принято все знаки корня подстраивать под самое высокое из них.

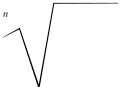
Знак корня используют только для выражений, помещающихся в пределах строки, а для более длинных вместо применяют эквивалентную запись . Впрочем, в некоторых руководствах по набору и вёрстке упоминается разрыв подкоренного выражения на несколько строк; при этом знак корня ставится над первой, а над продолжением подкоренного выражения ставится черта; в месте разрыва строк и знак корня, и черта над продолжением снабжаются стрелками, обращёнными наружу.

Примечания
  1. Элементарная математика, 1976, с. 49.
  2. Корн Г., Корн Т. Справочник по математике, 1970, с. 33.
  3. Florian Cajori. A History Of Mathematical Notations. — The Open Court Company, 1928. — Т. 1. — С. 150.
  4. Valentin Zaitsev, Andrew Janishewsky, Alexander Berdnikov: Russian Typographical Traditions in Mathematical Literature. In: EuroTeX'99 proceedings. Архивная копия от 28 сентября 2012 на Wayback Machine (PDF 196 KB, english)

Литература

Ссылки
  • √ на сайте Scriptsource.org (англ.)
  • ∛ на сайте Scriptsource.org (англ.)
  • ∜ на сайте Scriptsource.org (англ.)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.