Метод прямоугольников
Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0. (Для формулы средних прямоугольников равен 1).
Если отрезок является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по
- Формуле левых прямоугольников:
- Формуле правых прямоугольников:
- Формуле прямоугольников (средних):
Составные квадратурные формулы
В случае разбиения отрезка интегрирования на элементарных отрезков приведённые выше формулы применяются на каждом из этих элементарных отрезков между двумя соседними узлами. В результате, получаются составные квадратурные формулы
- Для левых прямоугольников:
- Для правых прямоугольников:
- Для средних прямоугольников:
Формулу с вычислением значения в средней между двумя узлами точке можно применять лишь тогда, когда подынтегральная функция задана аналитически, либо каким-нибудь иным способом, допускающим вычисление значения в произвольной точке. В задачах, где функция задана таблицей значений остаётся лишь вычислять среднее значение между интегралами, посчитанными по формулам левых и правых прямоугольников соответственно, что приводит к составной квадратурной формуле трапеций.
Поскольку составные квадратурные формулы являются ни чем иным, как суммами, входящими в определение интеграла Римана, при они сходятся к точному значению интеграла. Соответственно, с увеличением точность получаемого по приближённым формулам результата возрастает.
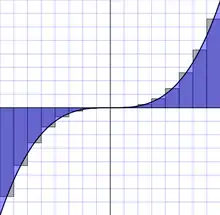
Составные формулы для равномерных сеток
Равномерную сетку можно описать следующим набором формул:
где — шаг сетки.
Для равномерных сеток формулы прямоугольников можно записать в виде следующих формул Котеса:
- Составная формула левых прямоугольников:
- Составная формула правых прямоугольников:
- Составная формула средних прямоугольников: Т.е. соответствует формуле трапеций.
Погрешность метода
Для формул правых и левых прямоугольников погрешность составляет
Для формулы прямоугольников (средних)
Для составных формул правых и левых прямоугольников на равномерной сетке:
Для составной формулы прямоугольников:
Пример реализации
Формула средних прямоугольников для аналитически заданной функции, написанная на С
double InFunction(double x) { //Подынтегральная функция
return sin(x);
}
double CalcIntegral(double a, double b, int n) {
double result = 0, h = (b - a) / n;
for(int i = 0; i < n; i++) {
result += InFunction(a + h * (i + 0.5));
}
result *= h;
return result;
}