Список квадратурных формул

В данной статье приведен список различных квадратурных формул, для численного интегрирования.

Обозначения

В общем виде формула численного интегрирования записывается следующим образом:

\int \limits _{\Omega _{x}}f(x)dx=\sum _{i=1}^{m_{g}}{{\widetilde {w_{i}}}f(x_{i})}=\sum _{i=1}^{m_{g}}{w_{i}\mathrm {det} (J(\xi _{i}))f(x(\xi _{i}))}

,

$f(x)$ — интегрируемая функция;
$w_{i}$ — веса интегрирования;
$\xi$ — система координат мастер-элемента;
$J(\xi )={\frac {\partial (x_{1},\dots ,x_{n})}{\partial (\xi _{1},\dots \xi _{n})}}$ — матрица Якоби для перехода на мастер-элемент.

В силу аддитивности интеграла в качестве области интегрирования $\Omega$ будут рассматриваться простые области (треугольник, четырёхугольник, тетраэдр и так далее), при сложной геометрии область можно представить как объединение простых и посчитать интеграл по ним или представить с помощью сплайна отображение на мастер-элемент.

В статье для обозначения естественных координат будут использоваться переменные $x,y,z$ , для обозначения координат мастер-элемента — $\xi ,\eta ,\zeta$ .

Одномерный интеграл

Численное интегрирование на мастер-элементе функции

x^{5}+6x^{2}+1

методом гаусса-3

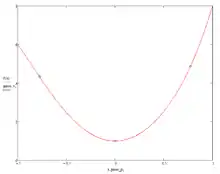
Одномерное интегрирование — это всегда интегрирование по отрезку.

Область интегрирования: отрезок $[x_{0},x_{1}]$ ;
Мастер-элемент: отрезок $[-1,1]$ ;
Переход на мастер-элемент: $\xi (x)=2{\frac {x-x_{0}}{x_{1}-x_{0}}}-1$ ;
Переход с мастер-элемента: $x(\xi )={\frac {(x_{1}-x_{0})(\xi +1)}{2}}+x_{0}$ ;
Якобиан: $\mathrm {det} (J(\xi ))={\frac {x_{1}-x_{0}}{2}}$ .

Номер	Число точек	Порядок интегрирования	$\xi$	$w$	Дополнительно
1	1	1	$0$	$2$	Метод прямоугольников
2	2	1	$-1$	$1$	Метод трапеций
2	2	1	$1$	$1$	Метод трапеций
3	2	3	$-{\frac {1}{\sqrt {3}}}$	$1$	Метод Гаусса-2
3	2	3	${\frac {1}{\sqrt {3}}}$	$1$	Метод Гаусса-2
4	3	3	$-1$	${\frac {1}{3}}$	Метод Симпсона
			$0$	${\frac {4}{3}}$
			$1$	${\frac {1}{3}}$
5	3	5	$-{\sqrt {\frac {3}{5}}}$	${\frac {5}{9}}$	Метод Гаусса-3
			$0$	${\frac {8}{9}}$
			${\sqrt {\frac {3}{5}}}$	${\frac {5}{9}}$
6	4	7	$-{\sqrt {{\frac {3}{7}}-{\frac {2}{7}}{\sqrt {\frac {6}{5}}}}}$	${\frac {18+{\sqrt {30}}}{36}}$	Метод Гаусса-4
			${\sqrt {{\frac {3}{7}}-{\frac {2}{7}}{\sqrt {\frac {6}{5}}}}}$	${\frac {18+{\sqrt {30}}}{36}}$
			$-{\sqrt {{\frac {3}{7}}+{\frac {2}{7}}{\sqrt {\frac {6}{5}}}}}$	${\frac {18-{\sqrt {30}}}{36}}$
			${\sqrt {{\frac {3}{7}}+{\frac {2}{7}}{\sqrt {\frac {6}{5}}}}}$	${\frac {18-{\sqrt {30}}}{36}}$
7	5	9	$0$	${\frac {128}{225}}$	Метод Гаусса-5
			$-{\frac {1}{3}}{\sqrt {5-2{\sqrt {\frac {10}{7}}}}}$	${\frac {322+13{\sqrt {70}}}{900}}$
			${\frac {1}{3}}{\sqrt {5-2{\sqrt {\frac {10}{7}}}}}$	${\frac {322+13{\sqrt {70}}}{900}}$
			$-{\frac {1}{3}}{\sqrt {5+2{\sqrt {\frac {10}{7}}}}}$	${\frac {322-13{\sqrt {70}}}{900}}$
			${\frac {1}{3}}{\sqrt {5+2{\sqrt {\frac {10}{7}}}}}$	${\frac {322-13{\sqrt {70}}}{900}}$

Двухмерный интеграл

Квадратный мастер-элемент

Квадратный мастер-элемент с изображенной 12-и точечной формулой

Область интегрирования: прямоугольник $[x_{0},x_{1}]\times [y_{0},y_{1}]$
Мастер-элемент: квадрат $[-1,1]\times [-1,1]$
Переход на мастер-элемент:

\xi (x,y)=2{\frac {x-x_{0}}{x_{1}-x_{0}}}-1

\eta (x,y)=2{\frac {y-y_{0}}{y_{1}-y_{0}}}-1

;

Переход с мастер-элемента:

x(\xi ,\eta )={\frac {(x_{1}-x_{0})(\xi +1)}{2}}+x_{0}

y(\xi ,\eta )={\frac {(y_{1}-y_{0})(\eta +1)}{2}}+y_{0}

;

Якобиан: $\mathrm {det} (J(\xi ,\eta ))={\frac {(x_{1}-x_{0})(y_{1}-y_{0})}{4}}$ .

Данные формулы интегрирования можно использовать и когда область интегрирования — выпуклый четырёхугольник, но тогда формулы перехода на мастер-элемент (и обратно) не будут иметь такой простой вид. Получить выражение для перехода можно используя интерполяционный полином.
Многие из формул интегрирования по квадрату можно получить, как комбинацию формул по отрезку: в качестве точек интегрирования берутся все возможные пары одномерных точек, а в качестве весов — соответствующие произведения весов интегрирования. Примерами таких методов в таблице ниже являются метод прямоугольников, метод трапеций и метод Гаусса-2.

Номер	Число точек	Порядок интегрирования	$\xi$	$\eta$	$w$	Дополнительно
1	1	1	$0$	$0$	$4$	Метод прямоугольников (метод среднего)
2	4	1	$-1$	$-1$	$1$	Метод трапеций
			$-1$	$1$	$1$

			$1$	$-1$	$1$
$1$	$1$	$1$
3	4	3	$-{\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$1$	Метод Гаусса-2
			$-{\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$1$

			${\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$1$
${\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$1$
4	12	7	$-c$	$0$	$w_{c}$	$a={\sqrt {\frac {114-3{\sqrt {583}}}{287}}}$ $b={\sqrt {\frac {114+3{\sqrt {583}}}{287}}}$ $c={\sqrt {\frac {6}{7}}}$ $w_{a}={\frac {307}{810}}+{\frac {923}{270{\sqrt {583}}}}$ $w_{b}={\frac {307}{810}}-{\frac {923}{270{\sqrt {583}}}}$ $w_{c}={\frac {98}{405}}$ Число узлов минимально[1].
			$c$	$0$	$w_{c}$

			$0$	$-c$	$w_{c}$

			$0$	$c$	$w_{c}$

			$-a$	$-a$	$w_{a}$

			$a$	$-a$	$w_{a}$

			$-a$	$a$	$w_{a}$
$a$	$a$	$w_{a}$
$-b$	$-b$	$w_{b}$
$b$	$-b$	$w_{b}$
$-b$	$b$	$w_{b}$
$b$	$b$	$w_{b}$

Треугольный мастер-элемент

Треугольный мастер-элемент, с точками Гаусса-4

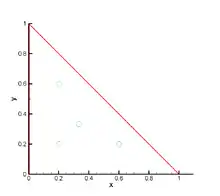
Область интегрирования: треугольник, образованный вершинами $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ ;
Мастер-элемент: треугольник, образованный вершинами $(0,0),(1,0),(0,1)$ .

Для перехода на мастер-элемент используются барицентрические координаты (L-координаты), обозначим их $\lambda _{1},\lambda _{2},\lambda _{3}$ .

\lambda _{i}(x,y)=\alpha _{i1}x+\alpha _{i2}y+\alpha _{i3}

Для вычисления коэффициентов L-координат используется матрица $D$ :

D={\begin{pmatrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\1&1&1\end{pmatrix}}

Матрица коэффициентов обратна к $D$ : $\mathrm {A} =D^{-1}$ .

Переход на мастер элемент:

\xi (x,y)=\lambda _{1}(x,y)

\eta (x,y)=\lambda _{2}(x,y)

Переход с мастер элемента:

{\begin{pmatrix}x\\y\\1\end{pmatrix}}=D{\begin{pmatrix}\xi \\\eta \\1-\xi -\eta \end{pmatrix}}

Якобиан : $\mathrm {det} (J(\xi ,\eta ))=\mathrm {det} (D)$ .

Номер	Число точек	Порядок интегрирования	$\xi$	$\eta$	$w$	Дополнительно
1	1	1	${\frac {1}{3}}$	${\frac {1}{3}}$	${\frac {1}{2}}$	Метод среднего
2	3	2	${\frac {1}{2}}$	$0$	${\frac {1}{6}}$	-
			$0$	${\frac {1}{2}}$	${\frac {1}{6}}$

${\frac {1}{2}}$	${\frac {1}{2}}$	${\frac {1}{6}}$
2	3	2	${\frac {1}{6}}$	${\frac {1}{6}}$	${\frac {1}{6}}$	Метод Гаусса-3
			${\frac {2}{3}}$	${\frac {1}{6}}$	${\frac {1}{6}}$

${\frac {1}{6}}$	${\frac {2}{3}}$	${\frac {1}{6}}$
4	4	3	${\frac {1}{3}}$	${\frac {1}{3}}$	$-{\frac {9}{32}}$	Метод Гаусса-4
			${\frac {3}{5}}$	${\frac {1}{5}}$	${\frac {25}{96}}$

			${\frac {1}{5}}$	${\frac {3}{5}}$	${\frac {25}{96}}$
${\frac {1}{5}}$	${\frac {1}{5}}$	${\frac {25}{96}}$
5	7	3	${\frac {1}{3}}$	${\frac {1}{3}}$	${\frac {9}{40}}$	Метод Ньютона-Котеса (англ. Newton-Cotes (англ.))
			${\frac {1}{2}}$	$0$	${\frac {1}{15}}$

			${\frac {1}{2}}$	${\frac {1}{2}}$	${\frac {1}{15}}$

			$0$	${\frac {1}{2}}$	${\frac {1}{15}}$

$1$	$0$	${\frac {1}{40}}$
$0$	$1$	${\frac {1}{40}}$
$0$	$0$	${\frac {1}{40}}$

Трёхмерный интеграл

Кубический мастер-элемент

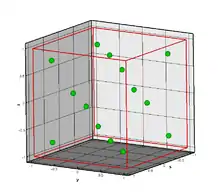
Кубический мастер-элемент, с изображенной 14-и точечной формулой

Область интегрирования: параллелепипед $[x_{0},x_{1}]\times [y_{0},y_{1}]\times [z_{0},z_{1}]$
Мастер-элемент: куб $[-1,1]\times [-1,1]\times [-1,1]$
Переход на мастер-элемент:

\xi (x,y,z)=2{\frac {x-x_{0}}{x_{1}-x_{0}}}-1

\eta (x,y,z)=2{\frac {y-y_{0}}{y_{1}-y_{0}}}-1

\zeta (x,y,z)=2{\frac {z-z_{0}}{z_{1}-z_{0}}}-1

Переход с мастер-элемента:

x(\xi ,\eta ,\zeta )={\frac {(x_{1}-x_{0})(\xi +1)}{2}}+x_{0}

y(\xi ,\eta ,\zeta )={\frac {(y_{1}-y_{0})(\eta +1)}{2}}+y_{0}

;

z(\xi ,\eta ,\zeta )={\frac {(z_{1}-z_{0})(\zeta +1)}{2}}+z_{0}

;

Якобиан: $\mathrm {det} (J(\xi ,\eta ,\zeta ))={\frac {(x_{1}-x_{0})(y_{1}-y_{0})(z_{1}-z_{0})}{8}}$ .

Аналогично как и для квадрата, куб можно использовать как мастер-элемент для произвольного шестигранника^{[уточнить]}, но тогда формулы перехода и якобиана усложнится.
Так же, аналогично с квадратом, многие формулы интегрирования по кубу можно получить из формул интегрирования по отрезку, координаты узлов — это все возможные тройки координат одномерной формулы, а веса интегрирования — произведение соответствующих весов одномерной формулы.

Номер	Число точек	Порядок интегрирования	$\xi$	$\eta$	$\zeta$	$w$	Дополнительно
1	1	1	$0$	$0$	$0$	$8$	Метод прямоугольников (метод среднего)
2	8	3	$-{\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$1$	Метод Гаусса-2
			$-{\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$1$

			$-{\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$1$

			$-{\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$1$

			${\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$1$
${\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$1$
${\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$-{\frac {1}{\sqrt {3}}}$	$1$
${\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	${\frac {1}{\sqrt {3}}}$	$1$
3	14	5	$-{\sqrt {\frac {19}{30}}}$	$0$	$0$	${\frac {320}{361}}$	Число узлов в классе формул с порядком аппроксимации 5 и не содержащих начало координат минимально.[2]
			${\sqrt {\frac {19}{30}}}$	$0$	$0$	${\frac {320}{361}}$
			$0$	$-{\sqrt {\frac {19}{30}}}$	$0$	${\frac {320}{361}}$
			$0$	${\sqrt {\frac {19}{30}}}$	$0$	${\frac {320}{361}}$
			$0$	$0$	$-{\sqrt {\frac {19}{30}}}$	${\frac {320}{361}}$
			$0$	$0$	${\sqrt {\frac {19}{30}}}$	${\frac {320}{361}}$
			$-{\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$
			$-{\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$
			$-{\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$
			$-{\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$
			${\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$
			${\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$
			${\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	$-{\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$
			${\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	${\sqrt {\frac {19}{33}}}$	${\frac {121}{361}}$

Поскольку формулы интегрирования высоких порядков содержат много точек, то их приведём отдельно.

Порядок: 7, число точек: 34

Номер точки	$\xi$	$\eta$	$\zeta$	$w$	Дополнительно
1	$a$	$0$	$0$	$w_{1}$	$a={\sqrt {\frac {6}{7}}}$ , $b={\sqrt {\frac {960-33{\sqrt {238}}}{2726}}}$ , $c={\sqrt {\frac {960+33{\sqrt {238}}}{2726}}}$ , $w_{1}={\frac {1078}{3645}}$ , $w_{2}={\frac {343}{3645}}$ , $w_{3}={\frac {43}{135}}+{\frac {829{\sqrt {238}}}{136323}}$ , $w_{4}={\frac {43}{135}}-{\frac {829{\sqrt {238}}}{136323}}$
2	$-a$	$0$	$0$	$w_{1}$
3	$0$	$a$	$0$	$w_{1}$
4	$0$	$-a$	$0$	$w_{1}$
5	$0$	$0$	$a$	$w_{1}$
6	$0$	$0$	$-a$	$w_{1}$
7	$a$	$a$	$0$	$w_{2}$
8	$a$	$-a$	$0$	$w_{2}$
9	$-a$	$a$	$0$	$w_{2}$
10	$-a$	$-a$	$0$	$w_{2}$
11	$a$	$0$	$a$	$w_{2}$
12	$a$	$0$	$-a$	$w_{2}$
13	$-a$	$0$	$a$	$w_{2}$
14	$-a$	$0$	$-a$	$w_{2}$
15	$0$	$a$	$a$	$w_{2}$
16	$0$	$a$	$-a$	$w_{2}$
17	$0$	$-a$	$a$	$w_{2}$
18	$0$	$-a$	$-a$	$w_{2}$
19	$b$	$b$	$b$	$w_{3}$
20	$b$	$b$	$-b$	$w_{3}$
21	$b$	$-b$	$b$	$w_{3}$
22	$b$	$-b$	$-b$	$w_{3}$
23	$-b$	$b$	$b$	$w_{3}$
24	$-b$	$b$	$-b$	$w_{3}$
25	$-b$	$-b$	$b$	$w_{3}$
26	$-b$	$-b$	$-b$	$w_{3}$
27	$c$	$c$	$c$	$w_{4}$
28	$c$	$c$	$-c$	$w_{4}$
29	$c$	$-c$	$c$	$w_{4}$
30	$c$	$-c$	$-c$	$w_{4}$
31	$-c$	$c$	$c$	$w_{4}$
32	$-c$	$c$	$-c$	$w_{4}$
33	$-c$	$-c$	$c$	$w_{4}$
34	$-c$	$-c$	$-c$	$w_{4}$

Тетраэдральный мастер-элемент

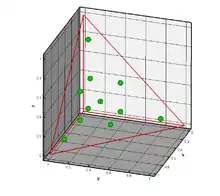
Тетраэдральный мастер-элемент с точками Гаусса-11

Область интегрирования: тетраэдр, образованный вершинами $(x_{1},y_{1},z_{1}),(x_{2},y_{2},z_{2}),(x_{3},y_{3},y_{3}),(x_{4},y_{4},z_{4})$ .
Мастер-элемент: тетраэдр, образованный вершинами $(0,0,0),(1,0,0),(0,1,0),(0,0,1)$ .

Аналогично с треугольником для перехода на мастер-элемент используются L-координаты тетраэдра, обозначим их $\lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4}$ :

\lambda _{i}(x,y,z)=\alpha _{i1}x+\alpha _{i2}y+\alpha _{i3}z+\alpha _{i4}

Матрица коэффициентов определяется, как: $\mathrm {A} =D^{-1}$ , где

D={\begin{pmatrix}x_{1}&x_{2}&x_{3}&x_{4}\\y_{1}&y_{2}&y_{3}&y_{4}\\z_{1}&z_{2}&z_{3}&z_{4}\\1&1&1&1\end{pmatrix}}

Переход на мастер-элемент:

\xi (x,y,z)=\lambda _{1}(x,y,z)

\eta (x,y,z)=\lambda _{2}(x,y,z)

\zeta (x,y,z)=\lambda _{3}(x,y,z)

Переход с мастер-элемента:

{\begin{pmatrix}x\\y\\z\\1\end{pmatrix}}=D{\begin{pmatrix}\xi \\\eta \\\zeta \\1-\xi -\eta -\zeta \end{pmatrix}}

Якобиан : $\mathrm {det} (J(\xi ,\eta ,\zeta ))=\mathrm {det} (D)$ .

Номер	Число точек	Порядок интегрирования	$\xi$	$\eta$	$\zeta$	$w$	Дополнительно
1	1	1	${\frac {1}{4}}$	${\frac {1}{4}}$	${\frac {1}{4}}$	${\frac {1}{6}}$	Метод среднего
2	4	2	${\frac {5+3{\sqrt {5}}}{20}}$	${\frac {5-{\sqrt {5}}}{20}}$	${\frac {5-{\sqrt {5}}}{20}}$	${\frac {1}{24}}$	Метод Гаусса-4
			${\frac {5-{\sqrt {5}}}{20}}$	${\frac {5+3{\sqrt {5}}}{20}}$	${\frac {5-{\sqrt {5}}}{20}}$	${\frac {1}{24}}$

			${\frac {5-{\sqrt {5}}}{20}}$	${\frac {5-{\sqrt {5}}}{20}}$	${\frac {5+3{\sqrt {5}}}{20}}$	${\frac {1}{24}}$
${\frac {5-{\sqrt {5}}}{20}}$	${\frac {5-{\sqrt {5}}}{20}}$	${\frac {5-{\sqrt {5}}}{20}}$	${\frac {1}{24}}$
3	5	3	${\frac {1}{4}}$	${\frac {1}{4}}$	${\frac {1}{4}}$	$-{\frac {2}{15}}$
			${\frac {1}{2}}$	${\frac {1}{6}}$	${\frac {1}{6}}$	${\frac {3}{40}}$
			${\frac {1}{6}}$	${\frac {1}{2}}$	${\frac {1}{6}}$	${\frac {3}{40}}$
			${\frac {1}{6}}$	${\frac {1}{6}}$	${\frac {1}{2}}$	${\frac {3}{40}}$
			${\frac {1}{6}}$	${\frac {1}{6}}$	${\frac {1}{6}}$	${\frac {3}{40}}$
4	11	4	${\frac {1}{4}}$	${\frac {1}{4}}$	${\frac {1}{4}}$	$-{\frac {74}{5625}}$	Метод Гаусса-11
			${\frac {11}{14}}$	${\frac {5}{70}}$	${\frac {5}{70}}$	${\frac {343}{45000}}$

			${\frac {5}{70}}$	${\frac {11}{14}}$	${\frac {5}{70}}$	${\frac {343}{45000}}$

			${\frac {5}{70}}$	${\frac {5}{70}}$	${\frac {11}{14}}$	${\frac {343}{45000}}$

			${\frac {5}{70}}$	${\frac {5}{70}}$	${\frac {5}{70}}$	${\frac {343}{45000}}$

			${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {56}{2250}}$

${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {56}{2250}}$
${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {56}{2250}}$
${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {56}{2250}}$
${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {56}{2250}}$
${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {1+{\sqrt {5/14}}}{4}}$	${\frac {1-{\sqrt {5/14}}}{4}}$	${\frac {56}{2250}}$
5	14	5	$a$	$a$	$a$	$A$	$A,\ B,\ C,\ a,\ b,\ c$ определяются из следующих уравнений: ${\begin{cases}t={\frac {4}{27}}\left(71-4{\sqrt {79}}\sin \left({\frac {1}{3}}\left[{\frac {\pi }{2}}+\arctan \left({\frac {27{\sqrt {10815}}}{67}}\right)\right]\right)\right)\\a={\frac {1+\alpha }{4}},\ b={\frac {1+\beta }{4}},\ c={\frac {1+2\gamma }{4}}\\\gamma ={\sqrt {1/t}},\ C=t^{2}/7!,\ \alpha >0\\A\alpha ^{2}+B\beta ^{2}=(1-t/21)/5!\\A\alpha ^{3}+B\beta ^{3}=-2/6!\\A\alpha ^{4}+B\beta ^{4}=10/7!\\A\alpha ^{5}+B\beta ^{5}=-6/7!\\\end{cases}}$ $A\approx 0.01878132095300264180$ $B\approx 0.01224884051939365826$ $C\approx 0.00709100346284691107$ $a\approx 0.31088591926330060980$ $b\approx 0.09273525031089122640$ $c\approx 0.45449629587435035051$
			$1-3a$	$a$	$a$	$A$
			$a$	$1-3a$	$a$	$A$
			$a$	$a$	$1-3a$	$A$
			$b$	$b$	$b$	$B$
			$1-3b$	$b$	$b$	$B$
			$b$	$1-3b$	$b$	$B$
			$b$	$b$	$1-3b$	$B$
			${\frac {1}{2}}-c$	$c$	$c$	$C$
			$c$	${\frac {1}{2}}-c$	$c$	$C$
			$c$	$c$	${\frac {1}{2}}-c$	$C$
			${\frac {1}{2}}-c$	${\frac {1}{2}}-c$	$c$	$C$
			${\frac {1}{2}}-c$	$c$	${\frac {1}{2}}-c$	$C$
			$c$	${\frac {1}{2}}-c$	${\frac {1}{2}}-c$	$C$

Примечания

Мысовских, 1981, с. 285.
Мысовских, 1981, с. 280.

Литература

Мысовских И. П. Интерполяционные кубатурные формулы. — Москва: Наука, 1981. — С. 336.

Ссылки

Numerical Integration over the Triangular Domain (англ.) (недоступная ссылка). — Интегрирование по треугольному элементу. Дата обращения: 12 июня 2014. Архивировано 14 июля 2014 года.
Numerical Integration over the Tetrahedral Domain (англ.) (недоступная ссылка). — Интегрирование по тетраэдальному элементу. Дата обращения: 12 июня 2014. Архивировано 14 июля 2014 года.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_c5180e5ece74fd5d-1] Мысовских, 1981, с. 285.

[_c5180e5ece74fd58-2] Мысовских, 1981, с. 280.