Гипотеза Фирузбэхт

Гипотеза утверждает, что ${\displaystyle p_{n}^{1/n}}$ (где ${\displaystyle p_{n}}$ — n-е простое число) является строго убывающей функцией от n, т. е.

${\displaystyle {\sqrt[{n+1}]{p_{n+1}}}<{\sqrt[{n}]{p_{n}}}}$ для всех ${\displaystyle n\geq 1.}$

Эквивалентно:

${\displaystyle p_{n+1}<p_{n}^{1+{\frac {1}{n}}}}$ для всех ${\displaystyle n\geq 1,}$

см. последовательности A182134, A246782.

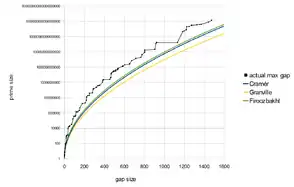
Используя таблицу максимальных интервалов, Фарида Фирузбэхт проверила свою гипотезу до 4,444⋅10¹²[2]. С расширенной таблицей максимальных промежутков гипотеза была проверена для всех простых чисел до ${\displaystyle 10^{19}}$[3][4].

Если гипотеза верна, то функция интервалов между простыми числами ${\displaystyle g_{n}=p_{n+1}-p_{n}}$ должна удовлетворять неравенству[5]:

${\displaystyle g_{n}<(\log p_{n})^{2}-\log p_{n}}$ для всех ${\displaystyle n>4.}$

Более того[6],

${\displaystyle g_{n}<(\log p_{n})^{2}-\log p_{n}-1}$ для всех ${\displaystyle n>9,}$

см. также последовательность A111943. Гипотеза находится среди наиболее сильных гипотез о верхних границах для интервалов между простыми числами, она даже несколько сильнее гипотез Крамера и Шенкса[4]. Из гипотезы вытекает сильная форма гипотезы Крамера, а потому она несовместима с эвристикой Гранвилла, Пинтца[7][8][9] и Майера[10][11], в которой предполагается, что

${\displaystyle g_{n}>{\frac {2-\varepsilon }{e^{\gamma }}}(\log p_{n})^{2}}$

встречается бесконечно много раз для любого ${\displaystyle \varepsilon >0,}$ где ${\displaystyle \gamma }$ означает константу Эйлера — Маскерони.

Две связанные гипотезы (см. комментарии к последовательности A182514)

${\displaystyle \left({\frac {\log(p_{n+1})}{\log(p_{n})}}\right)^{n}<e,}$

которая несколько слабее, и

${\displaystyle \left({\frac {p_{n+1}}{p_{n}}}\right)^{n}<n\log(n)}$ для всех ${\displaystyle n>5,}$

которая сильнее.

• Теорема о распределении простых чисел

• Hans Riesel. Prime Numbers and Computer Methods for Factorization, Second Edition (англ.). — Birkhauser, 1985. — ISBN 3-7643-3291-3.