Интервалы между простыми числами
Интервалы между простыми числами — это разности между двумя последовательными простыми числами. n-й интервал, обозначаемый , — это разность между (n + 1)-м и n-м простыми числами, то есть
Мы имеем: . Последовательность интервалов между простыми хорошо изучена. Иногда рассматривают функцию вместо
Первые 30 интервалов между простыми числами следующие:
Простые замечания
Для любого простого числа P, символом P# мы будем обозначать праймориал P, то есть произведение всех простых чисел, не превосходящих P. Если Q — это простое число, следующее за P, то последовательность
является последовательностью из последовательных составных чисел, поэтому существуют интервалы между простыми длины не меньше, чем . Следовательно, существуют сколь угодно большие интервалы между простыми числами, и для любого простого P существует n такое, что (Очевидно, что для этого мы можем выбрать n таким, что будет наибольшим простым числом, не превосходящим .). Другой способ увидеть, что существуют сколь угодно большие интервалы между простыми числами, использует тот факт, что множество простых чисел имеет нулевую плотность, согласно теореме о распределении простых чисел.
На самом деле, интервал между простыми величины P может встретиться между простыми, гораздо меньшими, чем P#. Например, самая первая последовательность из 71 последовательных составных чисел находится между 31398 и 31468, в то время как 71# является 27-значным числом.
Уже среднее значение интервалов между простыми растет как натуральный логарифм n.
С другой стороны, гипотеза о простых близнецах утверждает, что для бесконечно многих n.
Интервалы между простыми могут быть оценены сверху и снизу с помощью функции Якобсталя (последовательность A048670 в OEIS).
Численные результаты
На 2009 год наибольший известный интервал между числами, определёнными как вероятно простые, имеет длину 2 254 930, с 86 853-значными вероятно простыми был найден H. Rosenthal и J. K. Andersen[1].
Отношение M=gn/ln(pn) показывает, во сколько раз данный интервал gn отличается от среднего интервала между простыми вблизи простого числа pn. На 2017 год наибольшее известное значение M=41,93878373 обнаружено для интервала длиной 8350, следующего за 87-значным простым числом 293703234068022590158723766104419463425709075574811762098588798217895728858676728143227. Этот рекорд найден в процессе распределенных вычислений Gapcoin[2].
Отношение S=gn/ln2pn (oтношение Крамера — Шенкса — Грэнвилля) изучают в связи с гипотезой Крамера, утверждающей, что . Если не рассматривать аномально высокие значения S, наблюдающиеся для то наибольшее известное значение S=0,9206386 обнаружено для интервала длиной 1132, следующего за 16-значным простым числом 1693182318746371. Этот рекорд нашел в 1999 году Bertil Nyman[3] (последовательность A111943 в OEIS содержит это и все предшествующие простые числа , соответствующие рекордным значениям S).
Будем говорить, что является максимальным интервалом, если для всех будет . Meжду первыми простыми числами наблюдается приблизительно максимальных интервалов[4]; см. также последовательность A005250 в OEIS.
|
|
|
Наибольшие интервалы первых десяти тысяч
Уже во второй тысяче имеется интервал, длиной 34 числа, в котором нет простых чисел — (1327—1361). Причём, этот интервал удерживает свой рекорд длины до десятой тысячи. Лишь в девятой тысяче имеется второй интервал такой же длины — (8467—8501), а в десятой — более длинный интервал (36 чисел) — (9551—9587), который и является самым длинным интервалом первых десяти тысяч. Имеется также интервал длиной 32 числа — (5591—5623).
Дальнейшие результаты
Верхние оценки
Постулат Бертрана утверждает, что для любого k всегда существует хотя бы одно простое число между k и 2k, поэтому, в частности, , откуда .
Теорема о распределении простых чисел говорит, что «средняя длина» интервалов между простым p и следующим простым числом имеет порядок . Фактическая длина интервалов может быть больше или меньше этого значения. Однако, из теоремы о распределении простых чисел можно вывести, верхнюю оценку для длины интервалов простых чисел: для любого существует такое N, что для всех будет .
Хохайзель первым показал[5] что существует такое постоянное
- при
отсюда следует, что
для достаточно большого n.
Отсюда следует, что интервалы между простыми становятся сколь угодно меньше по отношению к простым: частное стремится к нулю при n стремящемся к бесконечности.
Hoheisel получил возможное значение 32999/33000 для . Эта оценка была улучшена до 249/250 Хайльброном[6], и до для любого Чудаковым[7].
Основное улучшение было получено Ингемом[8], который показал, что если
для некоторой константы , где O используется в смысле нотации O большое, то
для любого . Здесь, как обычно, обозначает дзета функцию Римана, а — функция распределения простых чисел не превосходящих x. Известно, что допускается , откуда в качестве можно взять любое число, большее . Из результата Ингама сразу следует, что всегда существует простое число между числами и для достаточно больших n. Заметим, что ещё не доказана гипотеза Линделёфа, которая утверждает, что в качестве c может быть выбрано любое положительное число, но из неё следует, что всегда существует простое число между и для достаточно больших n (см. также Гипотеза Лежандра). Если эта гипотеза верна, то возможно, что необходима ещё более строгая гипотеза Крамера. Одним из достигнутых приближений к гипотезе Лежандра является доказанный факт о том, что .[9]
Мартин Хаксли показал, что можно выбрать [10].
Последний результат принадлежит Бакеру, Харману и Пинцу, показавшим, что может быть взято равным 0,525.[9]
В 2005, Дэниел Голдстон, Янос Пинц и Джем Йылдырым доказали, что
и позже улучшили это[11] до
В 2013 Чжан Итан представил статью, где доказывается, что[12]
Этот результат многократно улучшался вплоть до
В частности, отсюда следует, что множество всех пар простых чисел, разницы между которыми не превосходит 246, бесконечно[13][14].
Нижние оценки
Роберт Ранкин доказал, что существует константа такая, что неравенство
сохраняется для бесконечно многих значений n. Наилучшее известное значение для c на текущий момент — это , где — постоянная Эйлера-Маскерони.[15] Пауль Эрдёш предложил приз в $5000 за доказательство или опровержение того, что константа c в неравенстве выше может быть сколь угодно большой.[16]
Гипотезы об интервалах между простыми числами
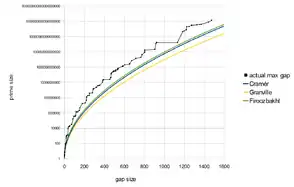
Здесь возможны ещё лучшие результаты, чем те, которые могут быть получены при предположении истинности гипотезы Римана. Харальд Крамер доказал, что если гипотеза Римана верна, то интервалы удовлетворяют соотношению
(здесь используется нотация O большое). Позже он предположил, что интервалы растут гораздо меньше. Грубо говоря, он предположил, что
В данный момент на это указывают численные расчеты. Для более детальной информации см. Гипотеза Крамера.
Гипотеза Андрицы утверждает, что
Это слабое усиление гипотезы Лежандра, которая утверждает, что между любой парой квадратов натуральных чисел существует хотя бы одно простое число.
Интервалы между простыми как арифметическая функция
Интервал между n-м и (n + 1)-м простым числом является примером арифметической функции. В таком контексте обычно её обозначают и называют разностью между простыми[16]. Разность между простыми не является ни мультипликативной, ни аддитивной арифметической функцией.
См. также
Примечания
- Largest known prime gap
- Nicely, T.R., New prime gap of maximum known merit. Дата обращения: 6 июня 2020.
- Nicely, T.R., First occurrence prime gaps. Дата обращения: 6 июня 2020.
- Kourbatov, А. On the nth record gap between primes in an arithmetic progression (англ.) // Int. Math. Forum : journal. — 2018. — Vol. 13, no. 2. — P. 65—78. — doi:10.12988/imf.2018.712103. — arXiv:1709.05508.
- Hoheisel, G. Primzahlprobleme in der Analysis (неопр.) // Sitzunsberichte der Koniglich Preussischen Akademie der Wissenschaften zu Berlin. — 1930. — Т. 33. — С. 3—11.
- Heilbronn, H. A. Uber den Primzahlsatz von Herrn Hoheisel (англ.) // Mathematische Zeitschrift : journal. — 1933. — Vol. 36, no. 1. — P. 394—423. — doi:10.1007/BF01188631.
- Tchudakoff, N. G. On the difference between two neighboring prime numbers (англ.) // Math. Sb. : journal. — 1936. — Vol. 1. — P. 799—814.
- Ingham, A. E. On the difference between consecutive primes (англ.) // Quarterly Journal of Mathematics : journal. — 1937. — Vol. 8, no. 1. — P. 255—266. — doi:10.1093/qmath/os-8.1.255.
- Baker, R. C.; Harman, G.; Pintz, G.; Pintz, J. The difference between consecutive primes, II (неопр.) // Proceedings of the London Mathematical Society. — 2001. — Т. 83, № 3. — С. 532—562. — doi:10.1112/plms/83.3.532.
- Huxley, M. N. On the Difference between Consecutive Primes (англ.) // Inventiones Mathematicae : journal. — 1972. — Vol. 15, no. 2. — P. 164—170. — doi:10.1007/BF01418933.
- arXiv:0710.2728
- Zhang, Yitang. Bounded gaps between primes (англ.) // Annals of Mathematics : journal. — Princeton University and the Institute for Advanced Study.
- Bounded gaps between primes. Polymath. Дата обращения: 21 июля 2013.>
- D.H.J. Polymath. Variants of the Selberg sieve, and bounded intervals containing many primes (англ.) // Research in the Mathematical Sciences : journal. — 2014. — Vol. 1. — doi:10.1186/s40687-014-0012-7. — arXiv:1407.4897.
- Pintz, J. Very large gaps between consecutive primes (англ.) // J. Number Theory : journal. — 1997. — Vol. 63, no. 2. — P. 286—301. — doi:10.1006/jnth.1997.2081.
- Guy, R. K. Unsolved problems in number theory (неопр.). — Third. — New York: Springer, 2004. — С. 31. — ISBN 0387208607.
Ссылки
- Thomas R. Nicely, Some Results of Computational Research in Prime Numbers — Computational Number Theory. This reference web site includes a list of all first known occurrence prime gaps.
- Weisstein, Eric W. Prime Difference Function (англ.) на сайте Wolfram MathWorld.
- http://planetmath.org/?op=getobj&from=objects&id=3143
- Chris Caldwell, Gaps Between Primes