Функция распределения простых чисел
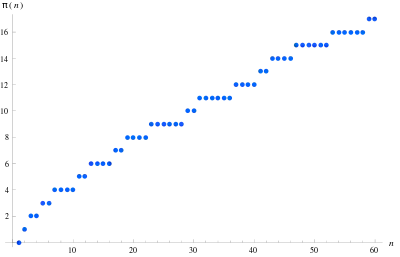
В математике функция распределения простых чисел, или пи-функция , — это функция, равная числу простых чисел, меньших либо равных действительному числу x.[1][2] Она обозначается (это никак не связано с числом пи).
История
Большой интерес в теории чисел представляет скорость роста пи-функции.[3][4] В конце XVIII столетия Гауссом и Лежандром было выдвинуто предположение, что пи-функция оценивается как
в смысле, что
Это утверждение — теорема о распределении простых чисел. Оно эквивалентно утверждению
где — это интегральный логарифм. Теорема о простых числах впервые была доказана в 1896 Жаком Адамаром и независимо Валле-Пуссеном, используя дзета-функцию Римана введенную Риманом в 1859.
Точнее рост сейчас описывается как
где обозначает O большое. Когда x не сильно велико больше, чем , однако разность меняет свой знак бесконечное число раз, наименьшее натуральное число, для которого происходит смена знака называется числом Скьюза.
Доказательства теоремы о простых числах, не использующие дзета-функцию или комплексный анализ, были найдены в 1948 году Атле Сельбергом и Паулем Эрдёшом (большей частью независимо).[5]
Таблицы для пи-функции, x / ln x и li(x)
В следующей таблице показан рост функций по степеням 10[3][6][7][8].
x π(x) π(x) − x / ln x li(x) − π(x) x / π(x) π(x)/x (доля простых чисел) 10 4 −0,3 2,2 2,500 40 % 102 25 3,3 5,1 4,000 25 % 103 168 23 10 5,952 16,8 % 104 1 229 143 17 8,137 12,3 % 105 9 592 906 38 10,425 9,59 % 106 78 498 6 116 130 12,740 7,85 % 107 664 579 44 158 339 15,047 6,65 % 108 5 761 455 332 774 754 17,357 5,76 % 109 50 847 534 2 592 592 1 701 19,667 5,08 % 1010 455 052 511 20 758 029 3 104 21,975 4,55 % 1011 4 118 054 813 169 923 159 11 588 24,283 4,12 % 1012 37 607 912 018 1 416 705 193 38 263 26,590 3,76 % 1013 346 065 536 839 11 992 858 452 108 971 28,896 3,46 % 1014 3 204 941 750 802 102 838 308 636 314 890 31,202 3,20 % 1015 29 844 570 422 669 891 604 962 452 1 052 619 33,507 2,98 % 1016 279 238 341 033 925 7 804 289 844 393 3 214 632 35,812 2,79 % 1017 2 623 557 157 654 233 68 883 734 693 281 7 956 589 38,116 2,62 % 1018 24 739 954 287 740 860 612 483 070 893 536 21 949 555 40,420 2,47 % 1019 234 057 667 276 344 607 5 481 624 169 369 960 99 877 775 42,725 2,34 % 1020 2 220 819 602 560 918 840 49 347 193 044 659 701 222 744 644 45,028 2,22 % 1021 21 127 269 486 018 731 928 446 579 871 578 168 707 597 394 254 47,332 2,11 % 1022 201 467 286 689 315 906 290 4 060 704 006 019 620 994 1 932 355 208 49,636 2,01 % 1023 1 925 320 391 606 803 968 923 37 083 513 766 578 631 309 7 250 186 216 51,939 1,92 % 1024 18 435 599 767 349 200 867 866 339 996 354 713 708 049 069 17 146 907 278 54,243 1,84 % 1025 176 846 309 399 143 769 411 680 3 128 516 637 843 038 351 228 55 160 980 939 56,546 1,77 % 1026 1 699 246 750 872 437 141 327 603 28 883 358 936 853 188 823 261 155 891 678 121 58,850 1,70 % 1027 16 352 460 426 841 680 446 427 399 267 479 615 610 131 274 163 365 508 666 658 006 61,153 1,64 %
В OEIS первая колонка значений — это последовательность A006880, — это последовательность A057835, а — это последовательность A057752.
Алгоритмы вычисления пи-функции
Простой способ найти , если не очень велико, — это использование решета Эратосфена выдающего простые, не превосходящие и подсчитать их.
Более продуманный способ вычисления был дан Лежандром: дан , если — различные простые числа, то число целых чисел, не превосходящих и не делящихся на все равно
(где обозначает целую часть). Следовательно, полученное число равно
если числа — это все простые числа, не превосходящие .
В 1870—1885 годах в серии статей Эрнст Майссель описал (и использовал) практический комбинаторный способ вычисления . Пусть — первые простых, обозначим число натуральных чисел, не превосходящих , которые не делятся ни на одно . Тогда
Возьмем натуральное , если и если , то
Используя этот подход, Майссель вычислил для .
В 1959 году Деррик Генри Лемер расширил и упростил метод Майсселя. Определим, для действительного и для натуральных величину как число чисел, не превосходящих m имеющих ровно k простых множителей, причем все они превосходят . Кроме того, положим . Тогда
где сумма явно всегда имеет конечное число ненулевых слагаемых. Пусть — целое, такое, что , и положим . Тогда и при . Следовательно
Вычисление может быть получено следующим способом:
С другой стороны, вычисление может быть выполнено с помощью следующих правил:
Используя этот метод и IBM 701, Лемер смог вычислить .
Дальнейшие усовершенствования этого метода были сделаны Lagarias, Miller, Odlyzko, Deleglise и Rivat.[9]
Китайский математик Hwang Cheng использовал следующие тождества:[10]
и, полагая , выполняя преобразование Лапласа обеих частей и применяя сумму геометрической прогрессии с , получил выражение:
Другие функции, подсчитывающие простые числа
Другие функции, подсчитывающие простые числа, также используются, поскольку с ними удобнее работать. Одна из них — функция Римана, часто обозначаемая как или . Она испытывает прыжок на 1/n для степеней простых , причем в точке прыжка её значение равно полусумме значений на обеих сторонах от . Эти дополнительные детали нужны для того, чтобы она могла быть определена обратным преобразованием Меллина. Формально, мы определим как
где p простое.
Мы также можем записать
где — функция Мангольдта и
Формула обращения Мёбиуса дает
Используя известное соотношение между логарифмом дзета-функции Римана и функцией Мангольдта , и используя формулу Перрона мы получим
Функция Римана имеет производящую функцию
Функции Чебышёва — это функции, подсчитывающие степени простых чисел с весом :
Формулы для функций, подсчитывающих простые числа
Формулы для функций, подсчитывающих простые числа, бывают двух видов: арифметические формулы и аналитические формулы. Аналитические формулы для таких функций были впервые использованы для доказательства теоремы о простых числах. Они происходят от работ Римана и Мангольдта и в общем известны как явные формулы.[11]
Существует следующее выражение для -функции Чебышёва:
где
Здесь пробегает нули дзета-функции в критической полосе, где действительная часть лежит между нулем и единицей. Формула верна для всех . Ряд по корням сходится условно, и может быть взят в порядке абсолютного значения возрастания мнимой части корней. Заметим, что аналогичная сумма по тривиальным корням дает последнее слагаемое в формуле.
Для мы имеем следующую сложную формулу
Опять же, формула верна для всех , где — нетривиальные нули зета-функции, упорядоченные по их абсолютному значению, и, снова, последний интеграл берется со знаком «минус» и является такой же суммой, но по тривиальным нулям. Выражение во втором члене может быть рассмотренно как , где — это аналитическое продолжение интегральной показательной функции на комплексную плоскость с ветвью, вырезанной вдоль прямой .
Таким образом, формула обращения Мёбиуса дает нам[12]
верное для , где
называется R-функцией также в честь Римана.[13] Последний ряд в ней известен как ряд Грама[14] и сходится для всех .
Сумма по нетривиальным нулям дзета-функции в формуле для описывает флуктуации , в то время как остальные слагаемые дают гладкую часть пи-функции,[15] поэтому мы можем использовать
как наилучшее приближение для для .
Амплитуда «шумной» части эвристически оценивается как , поэтому флуктуации в распределении простых могут быть явно представлены -функцией:
Обширные таблицы значений доступны здесь.[7]
Неравенства
Здесь выписаны некоторые неравенства для .
Левое неравенство выполняется при , а правое — при [16]
Неравенства для -го простого числа :
Левое неравенство верно при , а правое — при .
Имеет место следующая асимптотика для -го простого числа :
Гипотеза Римана
Гипотеза Римана эквивалентна более точной границе ошибки приближения интегральным логарифмом, а отсюда и более регулярному распределению простых чисел
В частности,[17]
Примечания
- Bach, Eric; Shallit, Jeffrey. Section 8.8 // Algorithmic Number Theory (неопр.). — MIT Press, 1996. — Т. 1. — С. 234. — ISBN 0-262-02405-5.
- Weisstein, Eric W. Prime Counting Function (англ.) на сайте Wolfram MathWorld.
- How many primes are there?. Chris K. Caldwell. Дата обращения: 2 декабря 2008. Архивировано 20 сентября 2012 года.
- Dickson, Leonard Eugene History of the Theory of Numbers I: Divisibility and Primality (англ.). — Dover Publications, 2005. — ISBN 0-486-44232-2.
- K. Ireland, M. Rosen. A Classical Introduction to Modern Number Theory (англ.). — Second. — Springer, 1998. — ISBN 0-387-97329-X.
- Tables of values of pi(x) and of pi2(x). Tomas Oliveira e Silva. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
- Values of π(x) and Δ(x) for various x's. Andrey V. Kulsha. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
- A table of values of pi(x). Xavier Gourdon, Pascal Sebah, Patrick Demichel. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
- Computing ?(x): The Meissel, Lehmer, Lagarias, Miller, Odlyzko method. Marc Deleglise and Joel Rivat, Mathematics of Computation, vol. 65, number 33, January 1996, pages 235–245. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
- Hwang H., Cheng. Demarches de la Geometrie et des Nombres de l'Universite du Bordeaux, Prime Magic conference.
- Titchmarsh, E.C. The Theory of Functions, 2nd ed (англ.). — Oxford University Press, 1960.
- Riesel, Hans; Gohl, Gunnar. Some calculations related to Riemann's prime number formula (англ.) // Mathematics of Computation : journal. — American Mathematical Society, 1970. — Vol. 24, no. 112. — P. 969—983. — ISSN 0025-5718. — doi:10.2307/2004630. — .
- Weisstein, Eric W. Riemann Prime Counting Function (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Gram Series (англ.) на сайте Wolfram MathWorld.
- The encoding of the prime distribution by the zeta zeros. Matthew Watkins. Дата обращения: 14 сентября 2008. Архивировано 20 сентября 2012 года.
- Rosser, J. Barkley; Schoenfeld, Lowell. Approximate formulas for some functions of prime numbers (англ.) // Illinois J. Math. : journal. — 1962. — Vol. 6. — P. 64—94. — ISSN 0019-2082.
- Lowell Schoenfeld. Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II (англ.) // Mathematics of Computation : journal. — American Mathematical Society, 1976. — Vol. 30, no. 134. — P. 337—360. — ISSN 0025-5718. — doi:10.2307/2005976. — .
Литература
- К. Прахар. Распределение простых чисел. — Мир, 1967.
- В. И. Зенкин. Распределение простых чисел. Элементарные методы. Калининград, 2008.
Ссылки
- Chris Caldwell, The Nth Prime Page at The Prime Pages.