Майссель, Эрнст
Даниэль Фридрих Эрнст Майссель (нем. Daniel Friedrich Ernst Meissel, 31 июля 1826 года, Эберсвальде, Бранденбург — 11 марта 1895 года, Киль, Германская империя) — немецкий астроном и математик.
| Эрнст Майссель | |
|---|---|
 | |
| Дата рождения | 31 июля 1826[1] |
| Место рождения | |
| Дата смерти | 11 марта 1895[1] (68 лет) |
| Место смерти | |
| Страна | |
| Научная сфера | теория чисел |
Жизнь
Майссель посещал гимназию Фридриха Вильгельма в Берлине и после окончания школы в 1847 году поступил в Берлинский университет имени Гумбольдта, где математику в то время преподавали Карл Густав Якоби и Петер Густав Лежён Дирихле.
В 1850 году в Галле защитил докторскую диссертацию («De serie quaedam Jacobiana»), и в дальнейшем сдал государственный экзамен на специальность преподавателя.
С 1852 работал преподавателем в Берлинской горной академии, а также преподавал в Берлинской академии архитектуры. В том же году он стал директором Королевского земского ремесленного училища в Изерлоне.
В 1871 году назначен директором реального училища города Киль, где и провел остаток своей карьеры.
В годы работы в Киле был постоянным членом немецкого «Общества поддержки воздухоплавания»[2].
Труды
Майссель проводил исследования в области теории чисел, математического анализа (дифференциальные уравнения, асимптотические события, тета-функции, эллиптические функции, функции Бесселя), сферической тригонометрии, а также изучал прикладные вопросы гидродинамики, проблемы трех тел в небесной механике и преломление света в атмосфере.
Получил известность благодаря серии статьей 1870—1885 годов, в которых был описан и применен на практике разработанный им комбинаторный метод вычисления значения функции . Майссель, который обладал развитым навыком проводить точные расчеты и работать со сложными уравнениями, вычислил значения для .
Его алгоритм впоследствии был доработан и упрощен Лемером, который подтвердил точность вычислений Майсселя (проводившего их во времена до изобретения компьютера): при полученное Майсселем значение 50 847 478 отличается от точного значения только на 56 в меньшую сторону.
В 1985 году Lagarias, Miller и Odlyzko путем применения метода решета аналитической теории чисел значительно повысили эффективность метода Майсселя[3] , а позднее алгоритм был ещё раз доработан другими авторами с привлечением дополнительных методов аналитической теории чисел.[4]
Проект полета к Северному полюсу
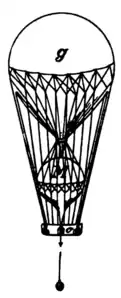
В 1866 году Майссель опубликовал свой проект полета к Северному полюсу на двухкамерном воздушном шаре (розьере), который в отличие от уже известных к тому времени проектов современников, имел в своей основе серьезные математические расчеты.
Основываясь на движении воздушных потоков, Майссель выбрал оптимальную конструкцию с одним шаром сверху, заполненным газом легче воздуха, для создания подъемной силы, и вторым шаром снизу, заполненным горячим воздухом. Нижний шар позволял расширить возможности управления летательным аппаратом за счет вертикального маневрирования.
Необходимый объем верхнего шара был оценен Майсселем в 22 500 м³, нижнего — в 3 750 м³. Потери газа в верхнем шаре должны были компенсироваться за счёт прикрепленных в нижней части железных цилиндров с жидким аммиаком. Подогрев воздуха в нижнем шаре осуществлялся с помощью керосиновой горелки.
По расчетам Майсселя при движении со скоростью 450 километров в сутки команда из 12 взрослых мужчин, вылетев из Санкт-Петербурга, достигла бы Северного полюса через 7 с половиной дней. Всего же весь перелет занял бы 24 дня, с запасом продовольствия на 40 дней[5].
См. также
- Константа Майсселя — Мертенса
- Алгоритм Майсселя — Лемера
Литература
- J. Peetre: Outline of a scientific biography of Ernst Meissel (1826—1895), Historia Mathematica Band 22, 1995, S. 154—178.
Ссылки
- John J. O’Connor, Edmund F. Robertson: Ernst Meissel на сайте MacTutor History of Mathematics archive
- Публикации Э. Майсселя в Astrophysics Data System
- Некролог. Astronomische Nachrichten, Bd. 137 (1895), S. 239
Примечания
- Архив по истории математики Мактьютор
- Zeitschrift des Deutschen Vereins zur Förderung der Luftschiffahrt. — Berlin: Deutscher Verein zur Förderung der Luftschiffahrt, 1882. — С. 32. — 406 с.
- J. C. Lagarias, V. S. Miller and Odlyzko A. M.: Computing π(x): the Meissel-Lehmer method,
- Chris Caldwell: How many primes are there? Архивировано 20 сентября 2012 года. 1.2.
- Hermann Moedebeck. Beiträge zur Geschichte des Luftballons in der Nordpolarforschung (нем.) // Illustrierte Aeronautische Mitteilungen. — 1897. — S. 32.