Тета-функция
Тета-функции — это специальные функции от нескольких комплексных переменных. Они играют важную роль во многих областях, включая теории абелевых многообразий, пространства модулей и квадратичных форм. Они применяются также в теории солитонов. После обобщения к алгебре Грассмана функции появляются также в квантовой теории поля[1].
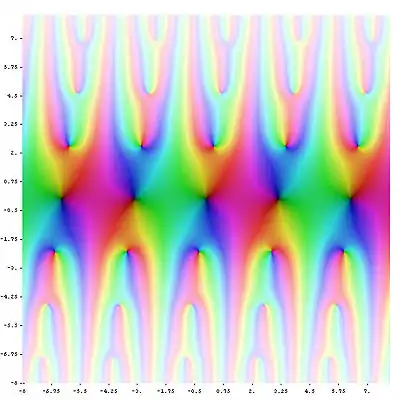
Наиболее распространённый вид тета-функций — это функции, встречающиеся в теории эллиптических функций. По отношению к одной из комплексных переменных (обычно обозначаемой z) тета-функция имеет свойство, выражающееся в сложении периодов ассоциированных эллиптических функций, что делает их квазипериодическими. В абстрактной теории это получается из условия линейного расслоения понижения.
Тета-функция Якоби



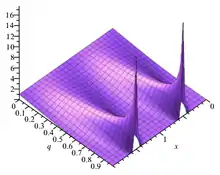
Имеется несколько связанных функций, которые называются тета-функциями Якоби, и много различных и несовместимых систем их обозначения. Одна тета-функция Якоби (названа именем Карла Густава Якоби), это функция, определённая от двух комплексных переменных z и , где z может быть любым комплексным числом, а ограничена верхней половиной плоскости, что означает, что число имеет положительную мнимую часть. Функция задаётся формулой
где и . Функция является формой Якоби. Если фиксировать , функция становится рядом Фурье для периодической целой функции от z с периодом 1. В этом случае тета-функция удовлетворяет тождеству
Функция ведёт себя очень регулярно с учётом квазипериода и удовлетворяет функциональному уравнению
где a и b — целые числа.
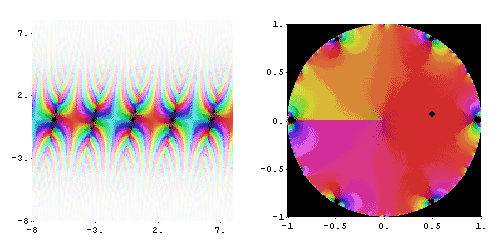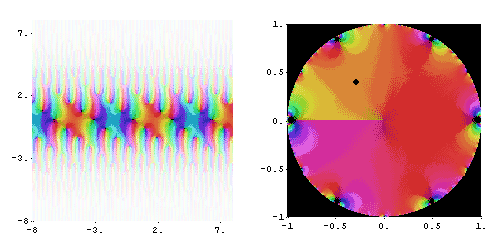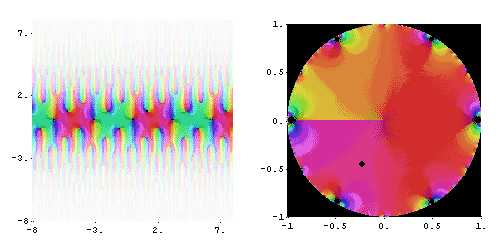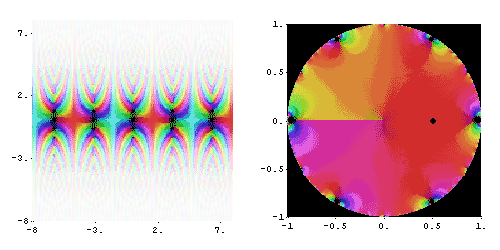

Вспомогательные функции
Тета-функция Якоби, определённая выше, иногда рассматривается вместе с тремя дополнительными тета-функциями и в этом случае записывается с дополнительным индексом 0:
Дополнительные (полупериодичные) функции определяются формулами
Этим обозначениям следовали Риман и Мамфорд. Первоначальная формулировка Якоби была в терминах нома , а не . В обозначениях Якоби θ-функции записываются в виде:
Приведённые выше определения тета-функции Якоби далеко не единственные. См. статью Тета-функции Якоби (вариации обозначений) с дальнейшим обсуждением.
Если мы положим в тета-функциях выше, мы получим четыре функции, зависящие только от и определённые на верхней полуплоскости (которые иногда называются тета-константами.) Они могут быть использованы для определения различных модулярных форм и для параметризации некоторых кривых. В частности, тождество Якоби
является кривой Ферма четвёртой степени.
Тождества Якоби
Тождества Якоби описывают, как тета-функции преобразуются модулярной группой, которая порождается отображениями и . Тождества для первого преобразования найти легко, поскольку добавление единицы в показателе к имеет тот же эффект, что и добавление к z ( mod 2). Во втором случае положим
Тогда
Тета-функции в терминах нома
Вместо выражения тета-функций в терминах z и мы можем выразить их в терминах аргумента w и нома q, где , а . В этом случае функции превращаются в
Мы видим, что тета-функции можно определить в терминах w и q без прямой ссылки на экспоненциальную функцию. Формулы могут быть использованы, поэтому, для определения тета-функций над другими полями, где экспоненциальная функция может быть не везде определена, такими как поле p-адических чисел.
Представления произведений
Тройное произведение Якоби (специальный случай тождеств Макдональда) говорит нам, что для комплексных чисел w и q с и мы имеем
Это можно доказать элементарными средствами, как, например, в книге Харди и Райта An Introduction to the Theory of Numbers.
Если мы выразим тета-функцию в терминах томов и , то
Мы поэтому получаем формулу произведения для тета-функции вида
В терминах w и q:
где является q-символом Похгаммера, а является q-тета-функцией. Если раскрыть скобки, тройное произведение Якоби получит вид
что можно также переписать в виде
Эта формула верна для общего случая, но представляет особый интерес при вещественных z. Аналогичные формулы произведений для дополнительных тета-функций
Целочисленные представления
Тета-функции Якоби имеют следующие интегральные представления:
Некоторые тождества с рядами
Следующие два тождества для рядов доказал Иштван Мезо[3]:
Эти отношения выполняются для всех 0 < q < 1. Фиксируя значения q, мы получим следующие свободные от параметров суммы
Нули тета-функций Якоби
Все нули тета-функций Якоби являются простыми нулями и задаются следующим образом:
- ,
где m, n являются произвольными целыми.
Связь с дзета-функцией Римана
Соотношение
использовал Риман для доказательства функционального уравнения для дзета-функции Римана посредством преобразования Меллина
и можно показать, что преобразование инвариантно относительно замены s на 1 − s. Cоответствующий интеграл для z ≠ 0 дан в статье о дзета-функции Гурвица.
Связь с эллиптической функцией Вейерштрасса
Тета-функции использовал Якоби для построения (в виде, приспособленном для упрощения вычислений) его эллиптических функций как частные вышеприведённых четырёх тета-функций, и он мог их использовать также для построения эллиптических функций Вейерштрасса, поскольку
- ,
где вторая производная берётся по z, а константа c определена так, что ряд Лорана функции ℘(z) в точке z = 0 имеет нулевой постоянный член.
Связь с q-гамма функцией
Четвёртая тета-функция – а тогда и остальные – неразрывно связана с q-гамма-функцией Джексона соотношением[4].
Связь с эта-функцией Дедекинда
Пусть — эта-функция Дедекинда, а аргумент тета-функции представлен как ном . Тогда
и
См. также статью о модулярных функциях Вебера.
Эллиптический модуль
J-инвариант равен
- ,
а дополнительный эллиптический модуль равен
Решение теплового уравнения
Тета-функция Якоби является фундаментальным решением одномерного уравнения теплопроводности с пространственными периодическими граничными условиями[5]. Принимая вещественным, а с вещественным и положительным t, мы можем записать
- ,
что решает уравнение теплопроводности
Это решение в виде тета-функции является 1-периодическим по x, и при оно стремится к периодической дельта-функции или гребню Дирака в смысле распределений
- .
Общие решения для задачи с пространственными периодическими начальными значениями для уравнения теплопроводности могут быть получены путём свёртки начальных данных в с тета-функцией.
Связь с группой Гейзенберга
Тета-функция Якоби является инвариантом при действии дискретной подгруппы группы Гейзенберга. Эта инвариантность представлена в статье о тета-представлении группы Гейзенберга.
Обобщения
Если F является квадратичной формой от n переменных, то тета-функция, связанная с F, равна
с суммой по решётке целых чисел ℤn. Эта тета-функция является модулярной формой с весом (на надлежащим образом определённой подгруппе) модулярной группы. В разложении в ряд Фурье
числа называются числами представления формы.
Тета-функция Рамануджана
Риманова тета-функция
Пусть
является множеством симметричных квадратных матриц, мнимая часть которых положительно определена. ℍn называется верхним полупространством Зигеля и является многомерным аналогом верхней полуплоскости. n-Мерным аналогом модулярной группы является симплектическая группа Sp(2n,ℤ). Для . Роль n-мерного аналога конгруэнтных подгрупп играет
Тогда, если дано , тета-функция Римана определяется как
Здесь является n-мерным комплексным вектором, а верхний индекс T означает транспонирование. Тета-функция Якоби является тогда частным случаем с и , где является верхней полуплоскостью.
Тета-функция Римана сходится абсолютно и равномерно на компактных подмножествах .
Функциональное уравнение функции
которое выполняется для всех векторов и для всех }} и .
Ряд Пуанкаре
Ряд Пуанкаре обобщает тета-ряд на автоморфные формы применительно к произвольным фуксовым группам.
Примечания
- Тюрин, 2003.
- Yi, 2004, с. 381–400.
- Mező, 2013, с. 2401–2410.
- Mező, 2012, с. 692–704.
- Ohyama, 1995, с. 431–450.
Литература
- Yousuke Ohyama. Differential relations of theta functions // Osaka Journal of Mathematics. — 1995. — Т. 32, вып. 2. — С. 431–450. — ISSN 0030-6126.
- Milton Abramowitz, Irene A. Stegun. sec. 16.27ff. // Handbook of Mathematical Functions. — New York: Dover Publications, 1964. — ISBN 0-486-61272-4.
- Ахиезер Н. И. Элементы теории эллиптических функций. — Москва: «Наука» Главная редакция физико-математической литературы, 1970. — (Физико-математическая библиотека инженера). — ISBN 0-8218-4532-2.
- Hershel M. Farkas, Irwin Kra. ch. 6 // Riemann Surfaces. — New York: Springer-Verlag, 1980. — ISBN 0-387-90465-4.. (обсуждение тета-функции Римана)
- Hardy G. H., Wright E. M. An Introduction to the Theory of Numbers. — 4th. — Oxford: Clarendon Press, 1959.
- David Mumford. Tata Lectures on Theta I. — Boston: Birkhauser, 1983. — ISBN 3-7643-3109-7.
- James Pierpont. Functions of a Complex Variable. — New York: Dover Publications, 1959.
- Harry E. Rauch, Hershel M. Farkas. Theta Functions with Applications to Riemann Surfaces. — Baltimore: Williams & Wilkins, 1974. — ISBN 0-683-07196-3.
- William P. Reinhardt, Peter L. Walker. Theta Functions // NIST Handbook of Mathematical Functions / Frank W. L. Oliver, Daniel M. Lozier, Ronald F. Boisvert, Charles W. Clark. — Cambridge University Press, 2010. — ISBN 978-0521192255,.
- Whittaker E. T., Watson G. N. ch. 21 // A Course in Modern Analysis. — 4th. — Cambridge: Cambridge University Press, 1927. (история θ-функций Якоби)
- Jinhee Yi. Theta-function identities and the explicit formulas for theta-function and their applications // Journal of Mathematical Analysis and Applications. — 2004. — Т. 292. — С. 381–400. — doi:10.1016/j.jmaa.2003.12.009.
- István Mező. A q-Raabe formula and an integral of the fourth Jacobi theta function // Journal of Number Theory. — 2012. — Т. 133, вып. 2. — С. 692–704. — doi:10.1016/j.jnt.2012.08.025.
- István Mező. Duplication formulae involving Jacobi theta functions and Gosper's q-trigonometric functions // Proceedings of the American Mathematical Society. — 2013. — Т. 141, вып. 7. — С. 2401–2410. — doi:10.1090/s0002-9939-2013-11576-5.
Литература для дальнейшего чтения
- Тета-функции, Якоби эллиптические функции // Математическая энциклопедия / Виноградов И. В.. — Советская энциклопедия, 1985. — Т. 5. — (Энциклопедии, словари, справочники).
- Прасолов В. В., Соловьёв Ю. П. Алгебраические уравнения и тета-функции. — М.: МК НМУ, 1994.
- Hershel M. Farkas. Theta functions in complex analysis and number theory // Surveys in Number Theory / Krishnaswami Alladi. — Springer-Verlag, 2008. — Т. 17. — С. 57–87. — (Developments in Mathematics). — ISBN 978-0-387-78509-7.
- Bruno Schoeneberg. IX. Theta series // Elliptic modular functions. — Springer-Verlag, 1974. — Т. 203. — С. 203–226. — (Die Grundlehren der mathematischen Wissenschaften). — ISBN 3-540-06382-X.
- Тюрин А. Н. Квантование, классическая и квантовая теория поля и тета-функции. — М., 2003.
Ссылки
- Moiseev Igor. Elliptic functions for Matlab and Octave.