Гипотеза Крамера

Гипотеза Крамера основывается на вероятностной модели (существенно эвристической) распределения простых, в которой предполагается, что вероятность того, что натуральное число x является простым, равна примерно ${\displaystyle {\frac {1}{\ln x}}}$. Эта модель известна как Модель Крамера' простых. Крамер доказал в своей модели, что упомянутая гипотеза истинна с вероятностью 1[1].

Крамер также дал условное доказательство более слабого утверждения о том, что

${\displaystyle p_{n+1}-p_{n}=O({\sqrt {p_{n}}}\ln p_{n})}$

предполагая истинной гипотезу Римана[1].

С другой стороны, E. Westzynthius доказал в 1931 году, что величина пробелов между простыми более чем логарифмическая. То есть,[2]

${\displaystyle \limsup _{n\to +\infty }{\frac {p_{n+1}-p_{n}}{\ln p_{n}}}=\infty .}$

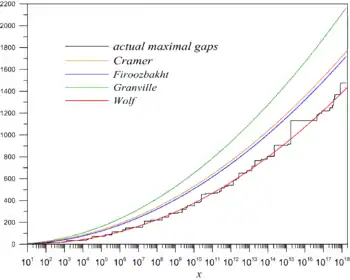
Даниэль Шенкс предложил гипотезу об асимптотическом равенстве для наибольших интервалов ${\displaystyle G(x)}$ между простыми, не превышающими ${\displaystyle x}$. Гипотеза Шенкса несколько сильнее, чем гипотеза Крамера:[3]

${\displaystyle G(x)\sim \ln ^{2}x.}$

В вероятностной модели,

${\displaystyle \limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{\ln ^{2}p_{n}}}=c,}$ с ${\displaystyle c=1.}$

Но константа ${\displaystyle c}$ возможно не такая, как для простых, по теореме Майера. Эндрю Гранвилл в 1995 году утверждал, что константа ${\displaystyle c=2e^{-\gamma }\approx 1.1229\ldots .}$[4], где ${\displaystyle \gamma }$ — постоянная Эйлера.

М. Вольф[5] предложил формулу для максимального расстояния ${\displaystyle G(x)}$ между последовательными простыми числами меньшими ${\displaystyle x}$. Формула Вольфа выражает ${\displaystyle G(x)}$ через функцию распределения простых чисел ${\displaystyle \pi (x)}$:

${\displaystyle G(x)\sim {\frac {x}{\pi (x)}}(2\ln \pi (x)-\ln x+c_{0}),}$

где ${\displaystyle c_{0}=\ln C_{2}=0.2778769...}$, а ${\displaystyle C_{2}=1.3203236...}$ есть удвоенная константа простых-близнецов.

Томас Найсли вычислил много наибольших пробелов между простыми.[6] Он проверил качество гипотезы Крамера, измерив отношение R логарифма простых к квадратному корню из размера пробела между простыми:

${\displaystyle R={\frac {\ln p_{n}}{\sqrt {p_{n+1}-p_{n}}}}.}$

Oн писал: «Для известных максимальных пробелов между простыми, R остаётся равным примерно 1,13,» что показывает, как минимум в диапазоне его вычислений, что грэнвиллево улучшение гипотезы Крамера не представляется лучшим приближением для имеющихся данных.

• Теорема о распределении простых чисел
• Интервалы между простыми числами
• Гипотеза Фирузбэхт — более сильная гипотеза
• Гипотеза Лежандра и гипотеза Андрицы — более слабые, но пока тоже не доказанные верхние оценки величины пробелов между простыми

• Weisstein, Eric W. Cramér Conjecture (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Cramér-Granville Conjecture (англ.) на сайте Wolfram MathWorld.