Геометрия (Декарт)
«Геометрия» (фр. La Géométrie) — труд Рене Декарта, опубликованный в Лейдене (Голландия) в 1637 году в качестве третьего приложения к философскому трактату Декарта «Рассуждение о методе». Число страниц: 106. Имя автора в первом издании не было указано. Это единственное сочинение Декарта, полностью посвящённое математике; оно рассматривалось автором как образец применения его общих методов. После 1637 года «Геометрия» издавалась отдельно от «Рассуждения о методе»[1].
| Геометрия | |
|---|---|
 Титульный лист | |
| Общая информация | |
| Автор | Рене Декарт |
| Тип | литературное произведение |
| Жанр | эссе |
| Оригинальная версия | |
| Название | фр. La Géométrie |
| Язык | французский |
| Место издания | Лейден |
| Издательство | Физматлит |
| Год издания | 1637 |
| Страниц | 106 |
| Русская версия | |
| Переводчик | А. П. Юшкевич |
| Автор комментариев | А. П. Юшкевич |
| Место издания | М.—Л. |
| Издательство | Гостехиздат |
| Год издания | 1938 |
| Страниц | 297 |
«Геометрия» Декарта стала поворотным пунктом в развитии новой математики, она была настольной книгой крупнейших математиков XVII века. Главной её ценностью было то, что книга содержала изложение нового раздела математики — аналитической геометрии, которая позволяла с помощью системы координат перевести геометрические задачи на алгебраический язык и тем самым существенно упрощала их исследование и решение. Кроме того, Декарт использовал в «Геометрии» удобную математическую символику, которая с этого момента стала общепринятой в науке. Наконец, «Геометрия» начала процесс переключения внимания математиков с изучения числовых величин на изучение зависимостей между ними — в современной терминологии, функций[2].
Революционные преобразования в математике, проведённые в «Геометрии», позволили Декарту решить ряд задач, недоступных старым методам. Декартовский подход послужил основой для разработки к концу XVII века Ньютоном и Лейбницем математического анализа.
Предыстория
В некотором смысле можно сказать, что Декарт поменял приоритеты алгебры и геометрии, исправив стратегическую ошибку древнегреческих математиков. В V веке до н. э. разразился первый кризис оснований математики[3] — пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, то есть их отношение () нельзя выразить ни натуральным числом, ни дробью. Однако других числовых объектов, кроме натуральных чисел, античные математики не признавали, даже дробь рассматривалась ими не как число, а как соотношение (пропорция). Найти выход сумел в IV веке до н. э. Евдокс Книдский — он ввёл, наряду с числами, понятие геометрических величин (длин, площадей, объёмов). Для однородных величин были определены арифметические операции, аналогичные числовым. Теория Евдокса была изложена Евклидом в пятой книге его «Начал», и она использовалась в Европе до XVII века. Теоремы о числах Евклиду приходилось отдельно передоказывать для величин, да и арифметика величин была существенно беднее, чем числовая — хотя бы потому, что касалась только однородных величин[4][5].
В Новое время выяснилось, что построение числовой алгебры на основе геометрии было ошибкой. Например, с точки зрения геометрии выражения и даже не имели геометрического истолкования (не определена физическая размерность величины-результата) и поэтому не имели смысла; то же относится к отрицательным числам[6].
Декарт пошёл иным путём — вместо сведе́ния алгебры к геометрии он свёл геометрию к алгебре, и этот путь оказался намного более плодотворным. Чтобы сделать это возможным, Декарт расширил понятие числа — оно вобрало все вещественные числа, включая иррациональные, и является отвлечённым, то есть отделено от геометрии[7]. Отдельное понятие геометрической величины тогда становится излишним. Алгебраизация геометрии позволила, кроме того, обнаружить общие черты в геометрических задачах, которые казались совершенно независимыми[8][9].
В сочетании с символической алгеброй Франсуа Виета и хорошо развитой к этому моменту системой алгебраических обозначений (в развитии которой и сам Декарт принимал участие) это новшество позволяло проводить математические исследования невиданной ранее глубины и общности. Впервые план такой реформы математики Декарт изложил 26 марта 1619 года в письме голландскому математику Исааку Бекману. Дополнительный материал Декарт получил в ходе своих занятий оптикой[10].
Предшественники
Декарт практически не ссылается в «Геометрии» на труды других учёных, что дало повод Валлису и нескольким другим математикам обвинить его в плагиате идей других алгебраистов, в частности, Хэрриота и Жирара. Впрочем, другой свой трактат, «Диоптрика», Декарт также построил так, как будто до него математической оптикой никто не занимался[11][12].
Несомненное влияние на Декарта оказал Франсуа Виет, основатель символической алгебры. Как упоминалось выше, основные идеи своей реформы Декарт начал разрабатывать ещё в 1619 году, так что в узловых пунктах своей программы он вполне самостоятелен. В этом убеждает также его обширная переписка. Жирар раньше Декарта сформулировал основную теорему алгебры (1629), а Хэрриот первым исследовал разложение многочлена на линейные множители (1631). Математическую символику Жирара и Хэрриота Декарт не применял, а с книгой Хэрриота ознакомился уже после выхода в свет «Геометрии». Декарт активно переписывался с Пьером Ферма, который также может претендовать на честь открытия аналитической геометрии, однако влияние Ферма в трудах Декарта не ощущается. Никто из предшественников не предложил столь радикальную реформу математики, как Декарт[13][14].
Идейные особенности подхода Декарта
Универсальный метод решения задач
При всей важности создания аналитической геометрии, публикацией «Геометрии» Декарт хотел добиться гораздо более масштабной цели — дать максимально общий метод решения математических задач. Этот общий (как он считал) метод Декарт излагает следующим образом. Большинство из математических задач в конечном счёте может быть сведено к алгебраическим уравнениям или системе таких уравнений. Поэтому решение задачи есть просто вычисление корней этих уравнений. Если при решении задачи возникают не алгебраические, а иные (трансцендентные) уравнения, то для них, полагал Декарт, общего метода решения не существует. Для фактического вычисления корней Декарт применяет графический метод — корни получаются как точки пересечения прямых, окружностей и других алгебраических кривых[15]. Декарту было известно, что построение двух кривых степеней и позволяет решить некоторое уравнение степени [16].
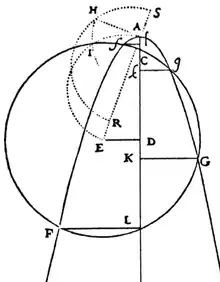
Например, чтобы решить уравнение:
Декарт представлял его в виде системы:
Первое уравнение даёт на плоскости (x, z) параболу, второе — окружность, и осталось найти точки их пересечения. Декарт показал, что аналогичными методами можно решать уравнения пятого и шестого порядка, для которых не существует алгебраических формул, подобных формуле Кардано[17].
Все выражения, входящие в уравнение, Декарт переносил в левую часть, так что правая часть всегда равна нулю; эта техника сводила исследование к нахождению корней многочлена в левой части и исследованию связи этих корней с коэффициентами уравнения[16].
Обобщение понятия числа
Как было показано выше, Декарт, в отличие от античных авторов, объединил числа и геометрические величины. При этом он различал три типа чисел: целые, дробные и иррациональные (лат. surdus, буквально: «глухие»); существенных различий между ними Декарт не делал, поскольку изучение непрерывных кривых и их алгебраических образов несовместимо с пифагорейским ограничением рациональными числами[18]. Декарт также сделал шаг к легализации отрицательных чисел, изображая их как отрезки, противоположные положительным. Хотя по традиции Декарт ещё называл отрицательные корни «ложными», он уже объединял их с «истинными», то есть положительными, в общую категорию «действительных корней» — противопоставляя их мнимым (комплексным) корням[19].
Реформа Декарта означала «уравнение в правах» целых, дробных и иррациональных чисел. Этот многолетний процесс завершил Ньютон, который в «Универсальной арифметике» (1707) дал классическое определение вещественного числа как отношения результата измерения к единичному эталону[19][20]:
Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой за единицу.
Оригинальный текст (лат.)[показатьскрыть]Per Numerum non tam multitudinem unitatum quam abstractam quantitatis cujusvis ad aliam ejusdem generis quantitattem quae pro unitate habetur rationem intelligimus.
Аналитическая геометрия
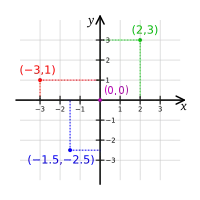
Зачатки координатного метода историки обнаружили в «Конических сечениях» Аполлония Пергского (III век до н. э.). Основные идеи аналитической геометрии сложились у Декарта не позднее 1632 года. Принцип формулировки геометрических свойств на алгебраическом языке одновременно с Декартом разрабатывал другой выдающийся французский математик, Пьер Ферма, но его работы не были опубликованы при жизни автора. Подход Ферма был аналогичен декартовскому, хотя уступал последнему по ясности и глубине изложения[21].
Координатная система Декарта несколько отличалась от современной. Декарт фиксирует на плоскости начало координат и положительную ось координат (он рассматривал только положительные координаты, причём ось ординат у него горизонтальна), затем проецирует на эту ось, перпендикулярно или под иным фиксированным углом, точки исследуемой кривой, фактически получая вторую координату (абсциссу) как длину проектирующего отрезка. Далее Декарт для этой кривой выводит соотношение, связывающее абсциссы и ординаты (уравнение кривой). После этого любое геометрическое утверждение о данной кривой можно вывести чисто алгебраически из уравнения кривой, не обращаясь к чертежам. Впрочем, отдавая дань древней традиции, Декарт обычно приводит и геометрическое истолкование своих уравнений. Отметим, что термины абсциссы, ординаты, координаты в современном смысле появились намного позднее у Лейбница, а вторую ось координат впервые ввёл комментатор Декарта Клод Рабуэль (Claude Rabuel, 1669—1728) в изданном посмертно (1730) дополнении к «Геометрии»[22][23][24][25].
Декарт разделил все непрерывные кривые на геометрические и механические; первые отличаются тем, что их можно описать алгебраическим уравнением. Механические кривые, такие как спирали или квадратрисы, Декарт вывел за пределы своего исследования. Он провёл первую в истории классификацию плоских алгебраических кривых разных степеней, впоследствии исправленную и дополненную Ньютоном[21]. Декарт ясно сознавал, что его алгебраизация таит в себе скрытую опасность — делая выводы из формулы для координат, надо, в принципе, каждый раз проверять, что эти выводы не зависят от выбора координатной системы и не являются случайным следствием какой-то особенности текущей системы координат. Рассуждения Декарта на эту тему положили начало теории инвариантов[9].
Обозначения Декарта
У Декарта алгебраическая символика получила практически современный вид; «Геометрия» — первая в истории книга, формулы в которой современный читатель воспримет без затруднений. Декарт предложил использовать для известных параметров начальные буквы алфавита: а для неизвестных — последние буквы: Ту же тройку Декарт использовал в качестве символов координат при построении графиков; сам Декарт, впрочем, ограничился плоскими кривыми, активное использование пространственных координат начал позднее Клеро[26][7].
Декарт сформировал современную запись возведения в степень, например: с показателем степени правее и выше символа переменной. Ближе к концу века Ньютон распространил эту запись на дробные и отрицательные показатели. Ф. Кэджори характеризует декартовскую запись степеней как самую удачную и гибкую символику во всей алгебре — она проста, компактна и наглядна, облегчает преобразования и, что оказалось особенно важным для дальнейшего, она стимулировала расширение понятия возведения в степень на отрицательные, дробные и даже комплексные показатели, а также появление в математике степенной и показательной функции; все эти достижения трудно было бы осуществить при использовании обозначений XVI века[27].
Алгебраическая символика Декарта почти полностью была принята последующими поколениями учёных, лишь необычный декартовский знак равенства ![]() был заменён на более удачный символ Роберта Рекорда. Кроме того, были сняты ограничения на коэффициенты, которые Декарт считал всегда неотрицательными, а исключения из этого правила отражал специальным значком[28]. Нидерландский математик Иоганн Худде уже в 1657 году позволил буквенным переменным принимать значения любого знака[29]. В монографии Ньютона «Универсальная арифметика» (1707) используются обозначения Декарта и знак равенства Рекорда. Унификация алгебраических обозначений к концу XVII века в основном завершилась[28].
был заменён на более удачный символ Роберта Рекорда. Кроме того, были сняты ограничения на коэффициенты, которые Декарт считал всегда неотрицательными, а исключения из этого правила отражал специальным значком[28]. Нидерландский математик Иоганн Худде уже в 1657 году позволил буквенным переменным принимать значения любого знака[29]. В монографии Ньютона «Универсальная арифметика» (1707) используются обозначения Декарта и знак равенства Рекорда. Унификация алгебраических обозначений к концу XVII века в основном завершилась[28].
Содержание
«Геометрия» делится на три части (книги). Утверждения автора, как правило, не сопровождаются строгими доказательствами, но иллюстрируются большим количеством примеров[16].
Книга первая: «О задачах, которые можно построить, пользуясь только кругами и прямыми линиями». Уже в первой главе автор заявляет: «Все задачи геометрии можно легко привести к таким терминам, что для их построения нужно будет затем знать лишь длину некоторых прямых линий». Декарт описывает соответствие между арифметическими операциями и эквивалентными им геометрическими построениями, знакомит читателя со своей системой обозначений. Далее он даёт метод построения уравнений для решаемой задачи — надо просто записать формулами данные в условии задачи соотношения и затем искать решение полученных уравнений[30].
В качестве примера эффективности своего метода Декарт рассмотрел и решил классическую задачу Паппа (из трактата Паппа «Математическое собрание», книга VII): для прямых на плоскости требуется найти геометрическое место таких точек, для которых произведение длин отрезков, проведённых из этих точек к данных прямых под одинаковыми углами, имеет заданное отношение к аналогичному произведению длин отрезков, проведённых к оставшимся прямым. Папп определил, что искомое геометрическое место является коническим сечением, однако полного доказательства не дал; Декарт же рассмотрел не только общий случай, но и особые ситуации (часть исследования помещена им в книгу вторую)[22][23][31].
Книга вторая: «О природе кривых линий». Эта книга посвящена приложениям алгебры к геометрии. Здесь Декарт указал общий метод проведения нормалей и касательных к алгебраическим кривым, который затем применил к некоторым задачам оптики. Дифференциальное исчисление ещё не было создано, и Декарт использует метод неопределённых коэффициентов, который иллюстрируется на примере эллипса, циссоиды Диокла и овала[32]. Когда Пьер Ферма сообщил Декарту свой дифференциальный метод проведения касательных, более простой и практически современный, тот его отверг как выходящий за пределы алгебры, хотя при исследовании циклоиды и логарифмической спирали он сам использовал методы, не укладывающиеся в декартовскую идеологию (например, метод неделимых)[33][34].
Декарт высказал в этой главе пессимизм в отношении возможности вычисления длины дуги произвольной кривой («спрямления кривой», как тогда говорили): по его мнению, «отношение между прямыми и кривыми неизвестно и, даже, думаю, не может быть познано людьми»[35][36], В то время действительно никакая кривая, кроме окружности, не поддавалась спрямлению. Пессимизм оказался неоправданным — двадцать лет спустя (в 1657 году) Уильям Нейл осуществил спрямление параболы Нейла, а ещё через год Рен нашёл длину арки неалгебраической циклоиды. Далее математический анализ создал общую теорию нахождения длины дуги, которая немедленно была использована для самых различных кривых[37].
В конце второй части Декарт пишет: «Я полагаю теперь, что ничего не пропустил из начал, необходимых для познания кривых линий». В действительности необозримые возможности, открытые аналитической геометрией, послужили лишь началом впечатляющего прогресса новой геометрии[23].
Книга третья: «О построении телесных или превосходящих телесные задач». В третьей книге Декарт изложил накопленные к этому периоду основные теоремы алгебры и приёмы решения уравнений, которые увязал в единую систему, с удобной общей символикой и терминологией. В частности, он сформулировал основную теорему алгебры: уравнение может иметь столько различных корней, какова его степень (комплексные корни Декарт называл «воображаемыми» и уделял им мало внимания)[38].
Далее даны (без доказательства) правило знаков Декарта для определения числа положительных и отрицательных корней по коэффициентам многочлена (строго доказано только в XVIII веке Лагранжем), а также правила для определения положения вещественных корней на числовой оси. Опередив на столетие Этьена Безу, Декарт показал, что если — корень многочлена то этот многочлен имеет множитель то есть может быть представлен в виде . Декарт сводит задачу трисекции угла к кубическому уравнению и решает его обычным своим методом, с помощью конических сечений[38].
Декарт выразил мнение, что уравнения третьей и более высокой степени решить с помощью циркуля и линейки, вообще говоря, невозможно; другими словами, общее кубическое уравнение нельзя решить, используя только квадратные (а не кубические) корни. Это утверждение оказалось верным, хотя рассуждения автора на эту тему малоубедительны и доказательной силы не имеют. Но Декарт правильно отметил, что решение циркулем и линейкой кубического уравнения с целочисленными коэффициентами и старшим коэффициентом 1 возможно, если это уравнение имеет вещественный корень (который, очевидно, будет целым числом). Декарт также исчерпывающе решил аналогичный вопрос для уравнения 4-й степени, построив его резольвенту 3-го порядка[39][40].
Историческое влияние
Завершая «Геометрию», Декарт шутливо заметил[41]:
И я надеюсь, что наши потомки будут благодарны мне не только за то, что я здесь разъяснил, но и за то, что мною было добровольно опущено, с целью предоставить им удовольствие самим найти это.
В самом деле, труд Декарта, особенно после выхода его латинского перевода (1649, Франс ван Схотен), сразу приобрёл многочисленных сторонников и вызвал множество публикаций, авторы которых следовали по пути, указанному Декартом, и активно развивали его идеи. «Геометрия» выдержала в течение XVII века четыре переиздания в Голландии и Германии. С каждым новым изданием текст Декарта обрастал обширными дополнениями и разъяснениями трудных мест, уже второе издание занимало два тома[1]. Сам Декарт после «Геометрии» в определённой степени отошёл от математики и отдавал предпочтение развитию своей метафизической натурфилософии (хотя в письмах друзьям дал решение множества задач)[33].
Среди первых идейных последователей Декарта были ван Схотен, Эразм Бартолин, Иоганн Худде, Флоримон де Бон. Несомненное влияние Декарта испытал Джон Валлис (1655), который опубликовал трактат с многозначительным названием «Всеобщая математика или полный курс арифметики» (Mathesis universalis sive arithmeticum opus integrum, 1657), впоследствии переработанный в «Трактат по алгебре» (1685). Валлис распространил алгебраизацию на метод неделимых (до этого чисто геометрический), близко подойдя к созданию интегрального исчисления[42].
Исаак Ньютон в молодости зачитывался «Геометрией» Декарта и даже ставил её выше «Начал» Евклида. В «Универсальной арифметике» Ньютона (1707) отделение алгебры от геометрии состоялось окончательно[38][43][44]. Как отмечал историк Карл Бойер, в своих первых публикациях по анализу Готфрид Лейбниц, осознанно или нет, подражал стилю декартовой «Геометрии»[45]; в одном из писем Лейбниц называет своими учителями Галилея, Декарта и Гюйгенса[46].
Хотя создание в конце XVII века математического анализа обесценило тезис Декарта об универсальности алгебраического подхода, расширение этого тезиса на новой, аналитической основе сохранило всё лучшее, что было в пионерской работе Декарта, и позволило успешно применить новую математику во многих естественных науках[47].
Публикации

Первоиздания
- 1637: первое издание, Лейден, без указания имени автора.
- 1649: латинский перевод (Франс ван Схотен).
- 1659—1661: второе латинское издание, Амстердам. Добавлены статьи ван Схотена, Эразма Бартолина, Иоганна Худде, Флоримона Де Бона, Яна де Витта и других.
- 1683: третье латинское издание, незначительно дополненное.
- 1695: четвёртое латинское издание, Франкфурт на Майне, с участием и дополнениями Якоба Бернулли.
Текст в сети
Русский перевод
- Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М.—Л.: Гостехиздат, 1938. — 297 с. — (Классики естествознания).
- Рене Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — Изд. 2-е, испр.. — М.: URSS, 2010. — 296 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-01070-2.
Примечания
- История математики, том II, 1970, с. 30.
- Юшкевич А. П. Декарт и математика, 1938, с. 257.
- Матвиевская Г. П. Учение о числе на средневековом Ближнем и Среднем Востоке. — Ташкент: ФАН, 1967. — С. 28. — 344 с. Вопреки названию, книга прослеживает историю понятия числа с самых древних времён.
- Колмогоров А. Н. Величина // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 1.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 78.
- Башмакова И. Г. Лекции по истории математики в Древней Греции // Историко-математические исследования. — М.: Физматгиз, 1958. — № 11. — С. 309—323.
- Юшкевич А. П. Декарт и математика, 1938, с. 279—282.
- Scott, J. F. The scientific work of René Descartes. — New York: Garland, 1987. — ISBN 0824046722.
- Mac Tutor.
- Из истории алгебры XVI-XVII вв, 1979, с. 147—148.
- Из истории алгебры XVI-XVII вв, 1979, с. 143—144.
- Стиллвелл Д. Математика и ее история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — С. 127. — 530 с.
- Юшкевич А. П. Декарт и математика, 1938, с. 205, 227, 290—292.
- Цейтен Г. Г., 1938, с. 211.
- История математики, том II, 1970, с. 33, 43.
- Юшкевич А. П. Декарт и математика, 1938, с. 281—282.
- Вилейтнер Г., 1960, с. 58.
- Юшкевич А. П. Декарт и математика, 1938, с. 283.
- История математики, том II, 1970, с. 35—36.
- Юшкевич А. П. Декарт и математика, 1938, с. 293.
- История математики, том II, 1970, с. 103—104.
- История математики, том II, 1970, с. 106—109.
- Юшкевич А. П. Декарт и математика, 1938, с. 287.
- Геометрия, 1938, с. 215.
- Вилейтнер Г., 1960, с. 232, 247.
- История математики, том II, 1970, с. 113.
- History of Mathematical Notations, vol. 1, 2007, §315.
- История математики, том II, 1970, с. 40—46.
- History of Mathematical Notations, vol. 2, 2007, §392.
- Геометрия, 1938, с. 14.
- Вилейтнер Г., 1960, с. 216—218.
- Юшкевич А. П. Декарт и математика, 1938, с. 285.
- Юшкевич А. П. Декарт и математика, 1938, с. 289.
- Вилейтнер Г., 1960, с. 218—221.
- Геометрия, 1938, с. 49.
- Оригинал цитаты на французском языке: «la proportion, qui est entre les droites & les courbes n'estant pas connuë, & mesme ie croy ne le pouuant estre par les hommes», см. Descartes, René. Discours de la méthode.... — 1637. — С. 340.
- История математики, том II, 1970, с. 191—192.
- История математики, том II, 1970, с. 42—45.
- Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I. — С. 135.
- Цейтен Г. Г., 1938, с. 221—223.
- Геометрия, 1938, с. 113.
- Цейтен Г. Г., 1938, с. 228—230.
- Вилейтнер Г., 1960, с. 222—238.
- Стиллвелл Д. Математика и ее история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — С. 166. — 530 с.
- Boyer C. B. The History of the Calculus and its conceptual development. — Dover Publications, inc, 1949. — P. 207—208. — 346 p.
- Филиппов М. М. Лейбниц: Его жизнь и деятельность: общественная, научная и философская деятельность. Глава III. — СПб. : Изд. Ф. Павленкова. — 96 с. — (ЖЗЛ; Вып. 129).
- Юшкевич А. П. Декарт и математика, 1938, с. 292—293.
Литература
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — 468 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — 208 с. — (История науки и техники).
- Цейтен Г. Г. История математики в XVI и XVII веках / Обработка, примечания и предисловие М. Выгодского. — Изд. 2-е. — М.—Л.: ОНТИ, 1938. — 456 с.
- Юшкевич А. П. Декарт и математика // Декарт Р. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М—Л.: Гостехиздат, 1938. — С. 257—294. — 297 с. — (Классики естествознания).
- Яновская С. А. О роли математической строгости в творческом развитии математики и специально о «Геометрии» Декарта // Историко-математические исследования. — М.: Наука, 1966. — № 17. — С. 151—184.
- Cajori F. A History of Mathematical Notations. Vol. 1 (1929 reprint). — NY: Cosimo, Inc., 2007. — xvi + 456 p. — ISBN 978-1-60206-684-7.
- Cajori F. A History of Mathematical Notations. Vol. 2 (1929 reprint). — NY: Cosimo, Inc., 2007. — xii + 392 p. — ISBN 978-1-60206-713-4.

