Жирар, Альбер
Альбе́р Жира́р (фр. Albert Girard, 1595—1632) — французский математик и музыкант, живший и работавший в Нидерландах. Ученик Стевина. Основная профессия: военный инженер, однако на протяжении всей своей жизни он всегда называл себя математиком. Труды в области алгебры, плоской и сферической тригонометрии[2].
| Альбер Жирар | |
|---|---|
| фр. Albert Girard | |
| Дата рождения | 11 октября 1595 |
| Место рождения | |
| Дата смерти | 8 декабря 1632[1] (37 лет) или 9 декабря 1632 (37 лет) |
| Место смерти | |
| Страна | |
| Научная сфера | математика |
| Альма-матер | |
Биография
О жизни Жирара известно немного. Родился во французской Лотарингии в протестантской семье, с детства увлекался музыкой, впоследствии профессионально играл на лютне. С 1610 года протестантское богослужение во Франции было запрещено, и многие протестанты были вынуждены покинуть страну. Точную дату переселения семьи Жирара в Нидерланды историкам выяснить не удалось[3]. Во всяком случае, в 1613 году Жирар уже жил в Амстердаме, в районе Галле.
12 апреля 1614 года в валлонской церкви он женился на Сюзанне де Нуэтт {Suzanne des Nouettes}. Зарабатывает на жизнь игрой на лютне, некоторую материальную помощь оказывают родственники. 5 февраля 1615 года в Амстердаме крестился его сын Даниил, первый из одиннадцати его детей[4]. Судя по письмам, всю жизнь Жирар грустил по покинутой Франции и жаловался, что не может прокормить свою семью[3].
С 1617 года Жерар учится в Лейденском университета, куда поступил в возрасте 22 лет; изучал он там в основном музыку. и математику. Сохранилась его переписка с другом Якобом Голиусом, обучавшимся там же, в ней они обсуждали различные научные вопросы.
По окончании университета Жирар служил военным инженером в армии принца Фредерика Генриха Оранского[3].
Когда Константин Гюйгенс (отец Христиана Гюйгенса) поздравил Голиуса с назначением на должность профессора математики, он похвалил работу Жирара, особенно в области рефракции. Жирар также завязал знакомство с такими крупнейшими нидерландскими и французскими учёными, как Виллеброрд Снелл, Симон Стевин и Пьер Гассенди. Последний после встречи с Жераром отметил, что они оба принимают «движение Земли» (то есть коперниканство).
Он планировал опубликовать восстановленную им версию утраченного труда Евклида «Поризмы», трактат по оптике и трактат о музыке; но опасался, что его финансы этого не позволят[5].
Альбер Жирар умер в возрасте всего 37 лет (1632 год), оставив жену беременной двенадцатым ребёнком[6]. Родители похоронили Жирара на кладбище Groote Kerk в Галле, под именем «Mr. Aelbert, ingenieur»[7].
Научная деятельность
Несмотря на раннюю кончину, Жерар успел сделать немало крупных математических открытий.
В труде 1625 года Жирар впервые заявил (без доказательства), что каждое простое число вида может быть представлено в виде суммы двух квадратов (теорема Ферма — Эйлера, Диксон называет её теоремой Жирара)[8].
В своём трактате по тригонометрии («Tables des Sinus, tangentes et secantes, avec un traicté succinct de la Trigonométrie tant des triangles plans, que sphéricques», Гаага, 1626) Жирар привёл в стройную систему все известные до него теоремы плоской и сферической тригонометрии и дал несколько новых. Ему также принадлежит теорема, что общая площадь вписанных в круг четырёхугольников, которые можно построить по данным четырём сторонам, меняя их порядок, равна произведению трёх различных диагоналей, разделённому на удвоенный диаметр круга. Этот труд дважды переиздавался (в 1627 и 1629 годах).
Одним из важнейших трудов Жирара стал небольшой трактат «Новое открытие в алгебре» (фр. Invention Nouvelle en l'Algèbre, 1629), написанный в военном походе. В этом трактате он одним из первых исследовал симметрические функции корней алгебраического уравнения и сформулировал основную теорему алгебры:
Все уравнения алгебры имеют столько решений, сколько их показывает наименование [степень] наивысшей величины.
Оригинальный текст (фр.)[показатьскрыть]Toutes les équations d'algèbre reçoivent autant de solutions que la dénomination de la plus haute quantité le démontre.— Girard A. Invention nouvelle en l'algèbre], Jansons, 1629, p. 38
При этом, опережая своё время, Жирар учитывал как вещественные корни (включая отрицательные), так и «воображаемые» (последний термин обозначал комплексные корни, пользу от которых Жирар особо оговорил). Первым описал геометрическое представление отрицательных чисел на числовой оси[2]. Задолго до Паскаля описал «треугольник Паскаля». Он также привёл в этой книге некоторые тождества, касающиеся симметрических многочленов. Позже Ньютон независимо открыл эти соотношения; они позволяют вычислять, согласно формулам Виета, суммы степеней всех корней многочлена, используя только его коэффициенты[9]. Эти исследования завершили Леонард Эйлер, Карл Фридрих Гаусс и Эдуард Варинг.
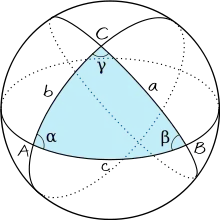
Вопреки названию трактата, Жирар привёл также несколько своих открытий в области геометрии и тригонометрии: в частности, он определил площадь сферического треугольника через его углы, указав, что эта площадь.пропорциональна «сферическому избытку» треугольника. та формула, независимо открытая Томасом Хэрриотом, впервые была опубликована Жираром. В 1632 году ту же формулу открыл Бонавентура Кавальери[10]., а затем Роберваль. Доказательство формулы было дано только в XVIII веке (Лежандр, Адриен Мари|Лежандр]] и Эйлер)[11]. Жирар исследовал также площади многоугольников и других фигур, образованных на поверхности сферы дугами круга.
В труде 1634 года Жирар впервые дал рекуррентную формулу ряда Фибоначчи и отметил, что отношения членов этой последовательности стремятся к золотому сечению.
Жирар перевёл на французский язык труды Диофанта, опубликовал сборник работ Симона Стевина (дополнив и улучшив работы Стевина, в том числе приведённые у Стевина тригонометрические таблицы).
Жирар ввёл в математику два классических обозначения: символ корня произвольной степени (до него символ радикала использовался только для квадратного корня) и знак плюс-минус. Он также систематически употреблял круглые скобки, что способствовало их признанию в науке. Он поддержал предложенные Николя Шюке названия «миллион», «миллиард» и «триллион». Наконец, Жирар первым ввёл в практику сокращения sin, cos, tan для синуса, косинуса и тангенса соответственно[3].
Труды
- 1625: Commentaires de l'édition des œuvres de Stevin, Arithmétique de Simon Stevin, revue, corrigée et augmentée de plusieurs traittez et annotations, par Albert Girard, sammielois, mathématicien, imprimé à Leyde, chez Jacques Elzevier. Seuls deux livres furent édités par Jacob ou Jacques Elzevier ; ces commentaires sont l'un d'eux '.
- 1625: Description et brève déclaration des règles générales de la fortification, l’artillerie, des munitions et vivres, des officiers et de leurs commissions, des retranchemens de camp, des approches, avec la manière de se deffendre, et des feux artificiels, par Henri Hondius. Le tout traduit du flamend en langue françoise par A. G. S., La Haye, Hendrik Hondius.
- 1626: Tables des Sinus, tangentes et secantes, avec un traicté succinct de la Trigonométrie tant des triangles plans, que sphéricques, par Albert Girard, sammielois, chez Jacques Elzevier à La Haye. Seconde édition 1634.
- 1627: Geometrie contenant la théorie et pratique d’icelle, nécessaire à la fortification. Jadis écrite par Samuel Marolois, mais depuis corrigée, et la plupart du discours changé et rédigé en meilleur état, par Albert Girard, mathématicien, Amsterdam, Jan Janssen.
- 1627: Fortification, ou architecture militaire, tant offensive que défensive par Samuel Marolois, revue, augmentée et corrigée par Albert Girard, Amsterdam, Jan Janssen. Réimpr. 1651, Труды этого автора можно найти в интернет-библиотеке Gallica. Следует произвести поиск (фр. Recherche) по фамилии. précédé de L’architecture contenant la Toscane, Dorique, Ionique, Corinthiaque et Composee, faict par Henri Hondius. Avec quelques belles ordonnances d’Architecture mises en perspective par Iean Vredman frison.
- 1628: Opera mathematica ou œuvres mathématiques..., De nouveau reveuë, augmentée, et corrigée par Albert Girard, Amsterdam], Jan Ianssen (numérisation). Réimpr. 1647,
- 1629: Invention nouvelle en l'algèbre, chez Jan Janssen}. Ce livre, dit Montucla, est « fort remarquable, en ce qu'on y trouve une connaissance des racines négatives plus développée que dans ceux de la plupart des autres analystes ». Un des objets de ce livre est de montrer que, dans les équations qui conduisent au cas irréductible, il y a toujours trois racines.
Издано посмертно
- 1634: Les œuvres mathématiques de Simon Stevin de Bruges, où sont insérés les mémoires mathématiques, auxquels s'est exercé le très haut et très illustre Prince Maurice de Nassau, prince d'Orange, gouverneur des Provinces des Pays-Bas etc., le tout revu, corrigé et augmenté par Albert Girard, sammiélois, mathématicien; publié à Leyde, chez Эльзевиры disponible sur diglib.
Примечания
- Архив по истории математики Мактьютор
- Математики. Механики, 1983, с. 183.
- MacTutor.
- Nederlandsch Biografisch Woordenboek (нид.). Дата обращения: 12 января 2021.
- Georges Maupin, Opinions et curiosités touchant la mathématique (deuxième série) d’après les ouvrages français des XVIe, XVIIe et XVIIIe siècle, Naud, Paris, 1898, pp. 246—247, Télécharger ici.
- Irem de l’université de Rennes, Équations du troisième et du second degré, Viète et Girard, chap. 12.
- Frédéric Métin. Albert Girard et le theoreme fondamental de l'algebre
- Dickson, Leonard Eugene. Chapter VI: Sum of two squares // History of the Theory of Numbers. — New York: Chelska Publishing Company, 1920. — P. 227—228.
- Albert Girard sur le site Fermat's Last Theorem.blogspot.com
- История математики, том II, 1970, с. 24.
- Terquem O. Nouveau manuel de géométrie, Librairie encyclopédique de Roret, 1838, p. 451.
Литература
- Боголюбов А. Н. Жирар Альбер // Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — С. 183. — 639 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
Ссылки
- Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Жирар, Альбер (англ.) — биография в архиве MacTutor.