Модель Удзавы — Лукаса

В модели рассматривается закрытая экономика. Фирмы максимизируют свою прибыль, а потребители — полезность. Экономика функционирует в условиях совершенной конкуренции. Производится только один продукт ${\displaystyle Y}$, используемый, как для потребления ${\displaystyle C}$, так и для инвестиций ${\displaystyle I}$. В качестве работника и потребителя в модели выступает бесконечно живущий индивид (или домохозяйство). Предполагается, что между разными поколениями существуют альтруистические связи, при принятии решений домохозяйство учитывает ресурсы и потребности не только настоящих, но и будущих своих членов, что делает его решения аналогичным решениям бесконечно живущего индивида. Фискальная политика в модели отсутствует. Время ${\displaystyle t}$ изменяется непрерывно[3].

Предпосылка о закрытой экономике означает, что произведенный продукт тратится на инвестиции и потребление, экспорт/импорт отсутствуют, сбережения равны инвестициям: ${\displaystyle S=I}$, ${\displaystyle C=cL}$, ${\displaystyle Y=C+I}$.

Производственная функция задается следующей формулой[3]:

${\displaystyle Y_{t}=AK_{t}^{\alpha }(uH_{t})^{1-\alpha }{\bar {h_{t}}}^{\beta }}$,

где ${\displaystyle A}$ — технологический параметр, ${\displaystyle A=const}$, ${\displaystyle K_{t}}$ — совокупный запас физического капитала, ${\displaystyle u}$ — доля населения, занятого в производстве, ${\displaystyle 0<u<1}$, ${\displaystyle {\bar {h_{t}}}^{\beta }}$ — внешний эффект от среднего уровня образования в экономике, ${\displaystyle 0<\beta <1}$, ${\displaystyle \alpha }$ — эластичность выпуска по физическому капиталу, ${\displaystyle 0<\alpha <1}$, ${\displaystyle H_{t}}$ — совокупный запас человеческого капитала, ${\displaystyle H_{t}=h_{t}L_{t}}$,

где ${\displaystyle L_{t}}$ — население равное в модели трудовым ресурсам, ${\displaystyle L=L_{0}e^{nt}}$, ${\displaystyle n=const}$, ${\displaystyle h_{t}}$ — уровень квалификации работников.

Для человеческого и физического капиталов выполняются условия отсутствия схемы Понци (финансовой пирамиды)[3]:

${\displaystyle \lim _{t\to \infty }K_{t}e^{-\int \limits _{0}^{t}(r(\nu )-n)d\nu }\geq 0}$,

${\displaystyle \lim _{t\to \infty }h_{t}L_{t}e^{-\int \limits _{0}^{t}(r(\nu )-n)d\nu }\geq 0}$,

где ${\displaystyle r}$ — ставка процента в экономике.

Индивид предлагает одну единицу труда (предложение труда неэластично) и получает натуральную заработную плату (в единицах товара). Функция полезности бесконечно живущего индивида-потребителя ${\displaystyle u(c_{t})}$ является сепарабельной, то есть потребление прошлых и будущих периодов не влияют на текущую полезность, влияет только потребление текущего периода. Она удовлетворяет условиям ${\displaystyle u'(c)>0,u''(c)<0}$ и условиям Инады (при потреблении, стремящемся к нулю, предельная полезность стремится к бесконечности, при потреблении, стремящемся к бесконечности, предельная полезность стремится к нулю): ${\displaystyle \lim _{c\to 0}u'(c)=+\infty$ ;\lim _{c\to \infty }u'(c)=0} , а также обладает постоянной эластичностью замещения ${\displaystyle {\frac {u''(c)}{u'(c)}}c=-\theta }$, и имеет вид[14]:

${\displaystyle U(c)=\int _{0}^{\infty }{\frac {c^{1-\theta }-1}{1-\theta }}e^{-(\rho -n)t}dt}$,

где ${\displaystyle \rho }$ — коэффициент межвременного предпочтения потребителя, ${\displaystyle \rho >0,\rho =const}$.

Сектор образования описывается следующим уравнением[15]:

${\displaystyle {\dot {h}}=\gamma (1-u)h_{t}}$,

где ${\displaystyle {\dot {h}}}$ — производная уровня квалификации по времени, ${\displaystyle (1-u)}$ — доля населения, занятого повышением квалификации, ${\displaystyle \gamma }$ — коэффициент производительности сектора образования, ${\displaystyle \gamma >0}$, ${\displaystyle \gamma =const}$.

Индивидуум принимает решение об уровне образования исходя из максимизации своего дохода ${\displaystyle z}$[15]:

${\displaystyle z=\int _{S}^{N}h(S)w_{t}e^{-rt}dt=\int _{S}^{N}e^{\gamma S+g_{w}t-rt}dt={\frac {e^{\gamma S+g_{t}N-rN}-e^{\gamma S+g_{w}S-rS}}{g_{w}-r}}\to max}$,

где ${\displaystyle N}$ — общий объём времени экономического агента, ${\displaystyle S}$ — время, потраченное на обучение, ${\displaystyle h(S)=e^{\gamma S}}$ — уровень образования индивида исходя из предпосылки ${\displaystyle {\dot {h}}=\gamma (1-u)h_{t}}$, ${\displaystyle w_{t}=e^{g_{w}t}}$— уровень заработной платы, где ${\displaystyle g_{w}={\frac {\dot {w}}{w}}}$ — темп роста заработной платы, ${\displaystyle g_{w}<r}$.

Условие максимума[16]:

${\displaystyle {\frac {\partial z}{\partial S}}={\frac {\gamma e^{\gamma S+g_{w}N-rN}-(\gamma +g_{w}-r)e^{\gamma S+g_{w}S-rS}}{g_{w}-r}}=0}$,

Решение этого уравнения в виде оптимального времени обучения ${\displaystyle S^{*}}$ выглядит следующим образом[16]:

${\displaystyle S^{*}=N-{\frac {1}{(g_{w}-r)}}ln(1+{\frac {g_{w}-r}{\gamma }})}$

Если принять дополнительную предпосылку о том, что экономический агент тратит на учёбу значительно меньшую часть своей жизни, чем на работу (${\displaystyle N>>S}$), или же, по аналогии с моделью пересекающихся поколений, считая, что человеческий капитал передается по наследству, а альтруистические связи между поколениями делают поведение домохозяйства аналогичным поведению бесконечно живущего индивида (${\displaystyle N\to \infty }$), мы получаем, что[16]:

${\displaystyle -{\frac {\gamma }{g_{w}-r}}=1\Rightarrow r=\gamma +g_{w}}$.

Задача потребителя в модели заключается в максимизации полезности при условии ограничений на темп роста капитала и на темп роста квалификации работников. Отдельный индивидуум в условиях совершенной конкуренции не влияет на средний уровень образования в экономике, потому в конкурентном равновесии ${\displaystyle {\frac {\partial {\bar {h_{t}}}}{\partial {h_{it}}}}=0}$[3][17].

${\displaystyle U(c)\to \max }$

при условиях:

${\displaystyle {\dot {K}}=I_{t}=Y_{t}-C_{t}=AK_{t}^{\alpha }(uh_{t}L_{t})^{1-\alpha }{\bar {h}}_{t}^{\beta }-cL_{t}}$,

${\displaystyle {\dot {h}}=\gamma (1-u)h_{t}}$,

${\displaystyle \lim _{t\to \infty }K_{t}e^{-\int \limits _{0}^{t}(r(\nu )-n)d\nu }\geq 0}$,

${\displaystyle \lim _{t\to \infty }h_{t}L_{t}e^{-\int \limits _{0}^{t}(r(\nu )-n)d\nu }\geq 0}$,

где ${\displaystyle {\dot {K}}}$ — производная запаса капитала по времени.

Для поиска равновесия составляется функция Гамильтона и находится её максимум при помощи принципа максимума Понтрягина[15].

Искомый равновесный темп роста выпуска ${\displaystyle g_{Y}^{*}={\frac {\dot {Y}}{Y}}}$ и потребления ${\displaystyle g_{C}^{*}={\frac {\dot {C}}{C}}}$ имеет следующий вид[3]:

${\displaystyle g_{C}^{*}=g_{Y}^{*}={\frac {(\gamma -\rho +n)(1-\alpha +\beta )}{\theta (1-\alpha )-(1-\theta )\beta }}+n}$.

Темп роста выпуска на душу населения ${\displaystyle g_{y}^{*}={\frac {\dot {y}}{y}}}$ и потребления и потребления на душу населения ${\displaystyle g_{c}^{*}={\frac {\dot {c}}{c}}}$ имеет следующий вид[21][3]:

${\displaystyle g_{c}^{*}=g_{y}^{*}={\frac {(\gamma -\rho +n)(1-\alpha +\beta )}{\theta (1-\alpha )-(1-\theta )\beta }}}$.

Равновесный темп роста заработной в модели платы ${\displaystyle g_{w}^{*}}$ имеет вид[22][3]:

${\displaystyle g_{w}^{*}={\frac {(\gamma -\rho +n)\beta }{\theta (1-\alpha )-(1-\theta )\beta }}}$.

Поскольку в модели присутствуют внешние эффекты, которые не учитываются потребителями при принятии решения об уровне образования (${\displaystyle {\frac {\partial {\bar {h_{t}}}}{\partial {h_{it}}}}=0}$), то децентрализованное равновесие не является оптимальным. Потому в модели при централизованном планировании можно достичь более высокого уровня потребления ${\displaystyle c}$. При централизованном планировании ${\displaystyle {\bar {h_{t}}}=h_{t}}$, и задача централизованного планирования выглядит следующим образом[3][23].

${\displaystyle U(c)\to \max }$

При условиях:

${\displaystyle {\dot {K}}=I_{t}=Y_{t}-C_{t}=AK_{t}^{\alpha }(uh_{t}L_{t})^{1-\alpha }h_{t}^{\beta }-cL_{t}}$,

${\displaystyle {\dot {h}}=\gamma (1-u)h_{t}}$,

${\displaystyle \lim _{t\to \infty }K_{t}e^{-\int \limits _{0}^{t}(r(\nu )-n)d\nu }\geq 0}$,

${\displaystyle \lim _{t\to \infty }h_{t}L_{t}e^{-\int \limits _{0}^{t}(r(\nu )-n)d\nu }\geq 0}$.

Для поиска равновесия составляется функция Гамильтона и находится её максимум при помощи принципа максимума Понтрягина[3].

Искомый равновесный темп оптимальный роста выпуска ${\displaystyle g_{Y}^{**}={\biggl (}{\frac {\dot {Y}}{Y}}{\biggr )}_{opt}}$ и потребления ${\displaystyle {\displaystyle g_{C}^{**}={\biggl (}{\frac {\dot {C}}{C}}{\biggr )}_{opt}}}$ имеет следующий вид[3]:

${\displaystyle g_{C}^{**}=g_{Y}^{**}={\frac {1}{\theta }}{\biggl (}\gamma {\frac {1-\alpha +\beta }{1-\alpha }}-\rho +n{\biggr )}+n}$.

Темп роста выпуска на душу населения ${\displaystyle g_{y}^{**}={\biggl (}{\frac {\dot {y}}{y}}{\biggr )}_{opt}}$ и потребления и потребления на душу населения ${\displaystyle g_{c}^{**}={\biggl (}{\frac {\dot {c}}{c}}{\biggr )}_{opt}}$ имеет следующий вид[24][3]:

${\displaystyle g_{c}^{**}=g_{y}^{**}={\frac {1}{\theta }}{\biggl (}\gamma {\frac {1-\alpha +\beta }{1-\alpha }}-\rho +n{\biggr )}}$.

Ставка процента ${\displaystyle r^{**}}$, соответствующая оптимальным темпам роста, имеет следующий вид[24][3]::

${\displaystyle r^{**}=\gamma {\frac {1-\alpha +\beta }{1-\alpha }}}$.

Таким образом, темпы роста потребления выпуска и заработной платы в модели при централизованном планировании выше, чем при конкурентном равновесии[24]. Однако при отсутствии внешнего эффекта от уровня образования (если ${\displaystyle \beta =0}$), темпы роста выпуска в централизованном и конкурентном состоянии совпадают и равны[24]:${\displaystyle g_{C}=g_{Y}={\frac {1}{\theta }}(\gamma -\rho +n)+n}$, а заработная плата не растет (${\displaystyle g_{w}=0}$), и модель превращается в полный аналог изначальной модели Удзавы.

Модель Узавы-Лукаса, равновесие и государственная политика

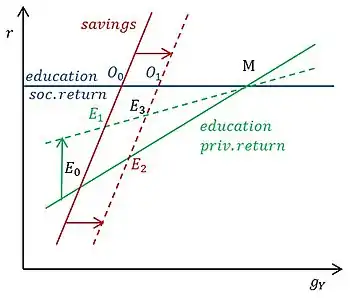
Графически равновесие в модели показано на иллюстрации. Синяя линия показывает общую отдачу от образования для экономики (${\displaystyle r^{**}}$). Зелёная линия показывает отдачу от образования для отдельного индивида. Красная линия обозначает финансовые ограничения индивида (сбережения). Точка ${\displaystyle E_{0}}$ — пересечение финансовых ограничений и отдачи от образования для индивида, конкурентное равновесие. Точка ${\displaystyle O_{0}}$ — пересечение финансовых ограничений и отдачи от образования для экономики, оптимальное (централизованное) равновесие. Точка ${\displaystyle M}$ — пересечение персональной и социальной отдачи от образования, максимально возможные темпы роста при текущем уровне внешних эффектов от образования ${\displaystyle \beta }$. Для темпов роста, превышающих темпы в точке ${\displaystyle M}$, необходимо, чтобы отдача от образования для индивида превышала общую отдачу от образования для экономики, что при положительном внешнем эффекте от образования невозможно[24].

Государственная политика может влиять на равновесие двумя способами. Первый вариант — стимулирование образования. Увеличение расходов на образование делает его производительность ${\displaystyle \gamma }$ выше, что сдвигает линию отдачи от образования для индивида (зелёную линию) вверх, равновесие сдвигается в точку ${\displaystyle E_{1}}$, приближая его к точке ${\displaystyle O_{0}}$: темпы роста ${\displaystyle g_{Y}}$и процентная ставка ${\displaystyle r}$ вырастут. Оптимальное равновесие не меняется[25].

Второй вариант — поощрение сбережений (в том числе и через повышение их доходности). в этом случае линию финансовых ограничений (красную линию) индивида вправо, равновесие сдвигается в точку ${\displaystyle E_{2}}$: темпы роста ${\displaystyle g_{Y}}$и процентная ставка ${\displaystyle r}$ вырастут. Однако оптимальное равновесие также изменится, оно сдвинется в точку ${\displaystyle O_{1}}$, приближаясь к точке ${\displaystyle M}$[26].

Возможно и одновременное применение обеих политик, тогда равновесие сдвинется в точку ${\displaystyle E_{3}}$, в которой темпы роста ${\displaystyle g_{Y}}$и процентная ставка ${\displaystyle r}$ выше, чем в точках ${\displaystyle E_{1}}$ и ${\displaystyle E_{2}}$[26].