Геометрическое распределение
Под Геометри́ческим распределе́нием в теории вероятностей подразумевают одно из двух распределений дискретной случайной величины:
- распределение вероятностей случайной величины равной номеру первого «успеха» в серии испытаний Бернулли и принимающей значения ;
- распределение вероятностей случайной величины равной числу «неудач» до первого «успеха» и принимающей значения .
Функция вероятности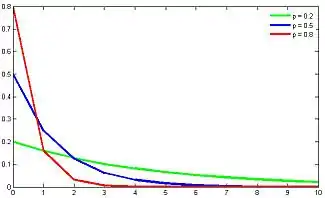 | ||
Функция распределения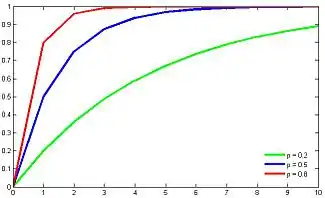 | ||
| Обозначение | ||
| Параметры | — число «неудач» до первого «успеха» — вероятность «успеха» — вероятность «неудачи» | — номер первого «успеха» — вероятность «успеха» — вероятность «неудачи» |
| Носитель | ||
| Функция вероятности | ||
| Функция распределения | ||
| Математическое ожидание | ||
| Медиана | N/A | N/A |
| Мода | ||
| Дисперсия | ||
| Коэффициент асимметрии | ||
| Коэффициент эксцесса | ||
| Информационная энтропия | ||
| Производящая функция моментов | ||
| Характеристическая функция | ||
Определение
- Говорят, что случайная величина имеет геометрическое распределение с параметром , и пишут , если принимает значения с вероятностями . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха .
- Пусть — бесконечная последовательность независимых случайных величин с распределением Бернулли, то есть
- .
- Построим случайную величину — число «неудач» до первого «успеха». Распределение случайной величины называется геометрическим с вероятностью «успеха» , что обозначается следующим образом: . Функция вероятности случайной величины имеет вид: .
Замечание
- Иногда полагают по определению, что — номер первого «успеха». Тогда функция вероятности принимает форму где . В таблице справа приведены формулы для обоих вариантов.
- Функция вероятности является геометрической прогрессией, откуда и происходит название распределения.
Моменты
Пусть и . Тогда производящая функция моментов геометрического распределения имеет вид:
- ,
откуда
- ,
- .
- Справедливо, что .
Свойства геометрического распределения
- Из всех дискретных распределений с носителем и фиксированным средним геометрическое распределение является одним из распределений с максимальной информационной энтропией.
- Если независимы и , то
- .
- Геометрическое распределение бесконечно делимо.
Отсутствие памяти
Если , то , то есть число прошлых «неудач» не влияет на число будущих «неудач».
Геометрическое распределение — это единственное дискретное распределение со свойством отсутствия памяти.
Связь с другими распределениями
- Геометрическое распределение является частным случаем отрицательного биномиального распределения: .
- Если независимы и , то
- .
- Если в отрицательном биномиальном распределении параметр r=1, то отрицательное биномиальное распределение становится геометрическим распределением. Последнее распределение является распределением Бозе-Эйнштейна для одного источника (a single source) [1]
Пример
Пусть игральная кость кидается до выпадания первой шестёрки.
- Рассчитайте вероятность того, что число испытаний, проводимых до первого успеха, включая последнее, успешное испытание будет не больше трёх.
- Положим . Тогда
- .
- Рассчитайте вероятность того, что число «неудач» до первого «успеха» будет не больше двух.
- Положим . Тогда
- .
См. также
Ссылки
- Schopper H. (Ed.) Electron - Positron Interactions. Berlin, Heidelberg: Springer-Verlag. 1992. P. 133// https://www.twirpx.org/file/3458790/
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.