Гамма-распределение
Га́мма-распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрла́нга.
| Гамма распределение | |
|---|---|
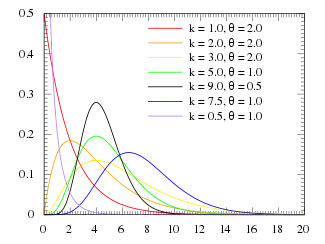 Плотность вероятности Плотность вероятности | |
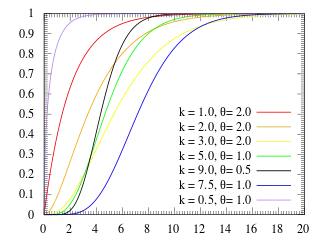 Функция распределения Функция распределения | |
| Обозначение | или [1] |
| Параметры | |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | Отсутствует явное выражение в закрытой форме |
| Мода | при |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Дифференциальная энтропия | |
| Производящая функция моментов | при |
| Характеристическая функция | |
Определение
Пусть распределение случайной величины задаётся плотностью вероятности, имеющей вид
- где — гамма-функция Эйлера.
Тогда говорят, что случайная величина имеет гамма-распределение с положительными параметрами и . Пишут .
Замечание. Иногда используют другую параметризацию семейства гамма-распределений. Или вводят третий параметр — сдвиг.
Моменты
Математическое ожидание и дисперсия случайной величины , имеющей гамма-распределение, имеют вид
- ,
- .
Свойства гамма-распределения
- Если — независимые случайные величины, такие что , то
- .
- Если , и — произвольная константа, то
- .
- Гамма-распределение бесконечно делимо.
Связь с другими распределениями
- Гамма-распределение является распределением Пирсона типа III[2].
- Экспоненциальное распределение является частным случаем гамма-распределения:
- .
- Если — независимые экспоненциальные случайные величины, такие что , то
- .
- Распределение хи-квадрат является частным случаем гамма-распределения:
- .
- Согласно центральной предельной теореме, при больших гамма-распределение может быть приближено нормальным распределением:
- при .
- Если — независимые случайные величины, такие что , то
- .
- Распределение Рэлея заменой переменной сводится к гамма-распределению.
- Обычное распределение Вейбулла заменой переменной сводится к гамма-распределению.
- Распределение Накагами заменой переменной сводится к гамма-распределению.
- Естественным обобщением гамма-распределения является усеченное гамма-распределение.
Моделирование гамма-величин
Учитывая свойство масштабирования по параметру θ, указанное выше, достаточно смоделировать гамма-величину для θ = 1. Переход к другим значениям параметра осуществляется простым умножением.
Используя тот факт, что распределение совпадает с экспоненциальным распределением, получаем, что если U — случайная величина, равномерно распределённая на интервале (0, 1], то .
Теперь, используя свойство k-суммирования, обобщим этот результат:
где Ui — независимые случайные величины, равномерно распределённые на интервале (0, 1].
Осталось смоделировать гамма-величину для 0 < k < 1 и ещё раз применить свойство k-суммирования. Это является самой сложной частью.
Ниже приведён алгоритм без доказательства. Он является примером выборки с отклонением.
- Положить m равным 1.
- Сгенерировать и — независимые случайные величины, равномерно распределённые на интервале (0, 1].
- Если , где , перейти к шагу 4, иначе к шагу 5.
- Положить . Перейти к шагу 6.
- Положить .
- Если , то увеличить m на единицу и вернуться к шагу 2.
- Принять за реализацию .
Подытожим:
где [k] является целой частью k, а ξ сгенерирована по алгоритму, приведённому выше при δ = {k} (дробная часть k); Ui и Vl распределены как указано выше и попарно независимы.
Примечания
- Родионов, 2015, с. 29.
- Королюк, 1985, с. 134.
Литература
- Лагутин М.Б. Наглядная математическая статистика. — М.: Бином, 2009. — 472 с.
- Жуковский М.Е., Родионов И.В. Основы теории вероятностей. — М.: МФТИ, 2015. — 82 с.
- Жуковский М.Е., Родионов И.В., Шабанов Д.А. Введение в математическую статистику. — М.: МФТИ, 2017. — 109 с.
- Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.