Бета-распределение
Бе́та-распределе́ние в теории вероятностей и статистике — двухпараметрическое семейство абсолютно непрерывных распределений. Используется для описания случайных величин, значения которых ограничены конечным интервалом.
| Бета-распределение | |
|---|---|
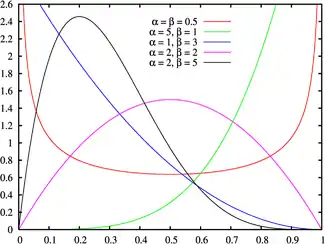 Плотность вероятности Плотность вероятности | |
 Функция распределения Функция распределения | |
| Обозначение | |
| Параметры |
|
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Мода | для |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Производящая функция моментов | |
| Характеристическая функция | |
Определение
Пусть распределение случайной величины задаётся плотностью вероятности , имеющей вид:
- ,
где
- произвольные фиксированные параметры, и
- — бета-функция.
Тогда случайная величина имеет бета-распределение. Пишут: .
Форма графика
Форма графика плотности вероятности бета-распределения зависит от выбора параметров и .
- — график выпуклый и уходит в бесконечность на границах (красная кривая);
- или — график строго убывающий (синяя кривая)
- — график строго выпуклый;
- — график является прямой линией;
- — график строго вогнутый;
- график совпадает с графиком плотности стандартного непрерывного равномерного распределения;
- или — график строго возрастающий (зелёная кривая);
- — график строго выпуклый;
- — график является прямой линией;
- — график строго вогнутый;
- — график унимодальный (пурпурная и чёрная кривые)
В случае, когда , плотность вероятности симметрична относительно (красная и пурпурная кривые), то есть
- .
Моменты
Математическое ожидание и дисперсия случайной величины , имеющей бета-распределение, имеют вид:
- ,
- .
Связь с другими распределениями
- Бета-распределение является распределением Пирсона типа I[1].
- Стандартное непрерывное равномерное распределение является частным случаем бета-распределения:
- .
- Бета-распределение широко используется в байесовской статистике, так как оно является сопряжённым априорным распределением для распределения Бернулли, биномиального и геометрического распределений.
- Если — независимые гамма-распределённые случайные величины, причём , а , то
- .
Примечания
- Королюк, 1985, с. 133.
Литература
- Королюк В.С., Портенко Н.И.,Скороход А.В., Турбин А.Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.