Вектор Лапласа — Рунге — Ленца
В классической механике ве́ктором Лапла́са — Ру́нге — Ле́нца называется вектор, в основном используемый для описания формы и ориентации орбиты, по которой одно небесное тело обращается вокруг другого (например, орбиты, по которой планета вращается вокруг звезды). В случае с двумя телами, взаимодействие которых описывается законом всемирного тяготения Ньютона, вектор Лапласа — Рунге — Ленца представляет собой интеграл движения, то есть его направление и величина являются постоянными независимо от того, в какой точке орбиты они вычисляются[1]; говорят, что вектор Лапласа — Рунге — Ленца сохраняется при гравитационном взаимодействии двух тел. Это утверждение можно обобщить для любой задачи с двумя телами, взаимодействующими посредством центральной силы, которая изменяется обратно пропорционально квадрату расстояния между ними. Такая задача называется Кеплеровой задачей[2].
- В этой статье векторы выделены жирным шрифтом, а их абсолютные величины — курсивом, например, .
Например, такой потенциал возникает при рассмотрении классических орбит (без учёта квантования) в задаче о движении отрицательно заряженного электрона, движущегося в электрическом поле положительно заряженного ядра. Если вектор Лапласа — Рунге — Ленца задан, то форма их относительного движения может быть получена из простых геометрических соображений, с использованием законов сохранения этого вектора и энергии.
Согласно принципу соответствия у вектора Лапласа — Рунге — Ленца имеется квантовый аналог, который был использован в первом выводе спектра атома водорода[3], ещё перед открытием уравнения Шрёдингера.
В задаче Кеплера имеется необычная особенность: конец вектора импульса всегда движется по кругу[4][5][6]. Из-за расположения этих кругов для заданной полной энергии проблема Кеплера математически эквивалентна частице, свободно перемещающейся в четырёхмерной сфере [7]. По этой математической аналогии сохраняющийся вектор Лапласа — Рунге — Ленца эквивалентен дополнительным компонентам углового момента в четырёхмерном пространстве[8].
Вектор Лапласа — Рунге — Ленца также известен как вектор Лапласа, вектор Рунге — Ленца и вектор Ленца, хотя ни один из этих учёных не вывел его впервые. Вектор Лапласа — Рунге — Ленца открывался вновь несколько раз[9]. Он также эквивалентен безразмерному вектору эксцентриситета в небесной механике[10]. Точно так же для него нет никакого общепринятого обозначения, хотя обычно используется . Для различных обобщений вектора Лапласа — Рунге — Ленца, которые определены ниже, используется символ .
Контекст
Одиночная частица, движущаяся под воздействием любой консервативной центральной силы, имеет по крайней мере четыре интеграла движения (сохраняющиеся при движении величины): полная энергия и три компоненты углового момента (вектора ). Орбита частицы лежит в плоскости, которая определяется начальным импульсом частицы, (или, что эквивалентно, скоростью ) и координатами, то есть радиус-вектором между центром силы и частицей (см. рис. 1). Эта плоскость перпендикулярна постоянному вектору , что может быть выражено математически с помощью скалярного произведения .
Как определено ниже, вектор Лапласа — Рунге — Ленца всегда находится в плоскости движения, то есть для любой центральной силы. Также является постоянным только для силы, зависящей обратно пропорционально квадрату расстояния[2]. Если центральная сила приблизительно зависит от обратного квадрата расстояния, вектор является приблизительно постоянным по длине, но медленно вращается. Для большинства центральных сил, однако, этот вектор не постоянный, а изменяет длину и направление. Обобщённый сохраняющийся вектор Лапласа — Рунге — Ленца может быть определён для всех центральных сил, но этот вектор — сложная функция положения и обычно не выражается аналитически в элементарных или специальных функциях[11][12].
История
Вектор Лапласа — Рунге — Ленца является сохраняющейся величиной в задаче Кеплера и полезен при описании астрономических орбит, наподобие движения планеты вокруг Солнца. Однако он никогда не был широко известен среди физиков, возможно, потому что является менее интуитивно понятным вектором, чем импульс и угловой момент. Вектор Лапласа — Рунге — Ленца независимо открывали несколько раз за прошедшие три столетия[9]. Якоб Герман был первым, кто показал, что сохраняется для специального случая центральной силы, зависящей обратно пропорционально квадрату расстояния[13], и нашёл его связь с эксцентриситетом эллиптической орбиты. Работа Германа была обобщена до её современной формы Иоганном Бернулли в 1710 году[14]. В свою очередь, Пьер-Симон Лаплас в конце XVIII столетия открыл сохранение вновь, доказав это аналитически, а не геометрически, как его предшественники[15].
В середине XIX века Уильям Гамильтон получил эквивалент вектора эксцентриситета, определённый ниже[10], использовав его, чтобы показать, что конец вектора импульса двигается по кругу под действием центральной силы, зависящей обратно пропорционально квадрату расстояния (рис. 3)[4]. В начале XX столетия Уиллард Гиббс получил тот же самый вектор с помощью векторного анализа[16]. Вывод Гиббса использовал Карл Рунге в популярном немецком учебнике по векторам в качестве примера[17], на который ссылался Вильгельм Ленц в своей статье о квантовомеханическом (старом) рассмотрении атома водорода[18].
В 1926 году этот вектор использовал Вольфганг Паули, чтобы вывести спектр атома водорода, используя современную матричную квантовую механику, а не уравнение Шрёдингера[3]. После публикации Паули вектор стал, главным образом, известен как вектор Рунге — Ленца.
Математическое определение

Для одиночной частицы, движущейся под действием центральной силы, зависящей обратно пропорционально квадрату расстояния и описываемой уравнением , вектор Лапласа — Рунге — Ленца определён математически по формуле[2]
где
- — масса точечной частицы, движущейся под воздействием центральной силы,
- — вектор импульса,
- — вектор углового момента,
- — параметр, описывающий величину центральной силы,
- — единичный вектор, то есть , где — радиус-вектор положения частицы, и — его длина.
Поскольку мы предположили, что сила консервативная, то полная энергия сохраняется
Из центральности силы следует, что вектор углового момента также сохраняется и определяет плоскость, в которой частица совершает движение. Вектор Лапласа — Рунге — Ленца перпендикулярен вектору углового момента и, таким образом, находится в плоскости орбиты. Уравнение верно, потому что вектора и перпендикулярны .
Это определение вектора Лапласа — Рунге — Ленца применимо для единственной точечной частицы с массой , движущейся в стационарном (не зависящем от времени) потенциале. Кроме того, то же самое определение может быть расширено на проблему с двумя телами, наподобие проблемы Кеплера, если заменить на приведённую массу этих двух тел и на вектор между этими телами.
Круговой годограф импульса
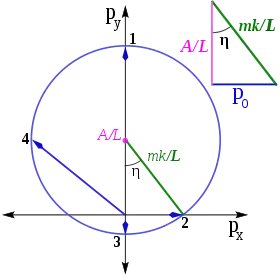
Сохранение вектора Лапласа — Рунге — Ленца и вектора углового момента используется в доказательстве того, что вектор импульса движется по кругу под действием центральной силы, обратно пропорциональной квадрату расстояния. Вычисляя векторное произведение и , приходим к уравнению для
Направляя вектор вдоль оси , а главную полуось — по оси , приходим к уравнению
Другими словами, вектор импульса ограничен окружностью радиуса , центр которой расположен в точке с координатами . Эксцентриситет соответствует косинусу угла , показанного на рис. 2. Для краткости можно ввести переменную . Круговой годограф полезен для описания симметрии проблемы Кеплера.
Интегралы движения и суперинтегрируемость
Семь скалярных величин: энергия и компоненты векторов Лапласа — Рунге — Ленца и момента импульса — связаны двумя соотношениями. Для векторов выполняется условие ортогональности , а энергия входит в выражение для квадрата длины вектора Лапласа — Рунге — Ленца, полученного выше . Тогда существует пять независимых сохраняющихся величин, или интегралов движения. Это совместимо с шестью начальными условиями (начальное положение частицы и её скорость являются векторами с тремя компонентами), которые определяют орбиту частицы, так как начальное время не определено интегралами движения. Поскольку величину (и эксцентриситет орбиты) можно определить из полного углового момента и энергии , то утверждается, что только направление сохраняется независимо. Кроме того, вектор должен быть перпендикулярным — это приводит к одной дополнительной сохраняющейся величине.
Механическая система с степенями свободы может обладать максимум интегралами движения, поскольку имеется начальных условий, а начальное время не может быть определено из интегралов движения. Система с более чем интегралами движения называется суперинтегрируемой, а система с интегралами называется максимально суперинтегрируемой[19]. Поскольку решение уравнения Гамильтона — Якоби в одной системе координат может привести только к интегралам движения, то переменные должны разделяться для суперинтегрируемых систем в больше чем одной системе координат[20]. Проблема Кеплера — максимально суперинтегрируема, так как она имеет три степени свободы () и пять независимых интегралов движения; переменные в уравнении Гамильтона — Якоби разделяются в сферических координатах и параболических координатах[21], как описано ниже. Максимально суперинтегрируемые системы могут быть квантованы с использованием только коммутационных соотношений, как показано ниже[22].
Уравнение Гамильтона — Якоби в параболических координатах
Постоянство вектора Лапласа — Рунге — Ленца можно вывести, используя уравнение Гамильтона — Якоби в параболических координатах , которые определяются следующим образом
где — радиус в плоскости орбиты
Обратное преобразование этих координат запишется в виде
Разделение переменных в уравнении Гамильтона — Якоби в этих координатах даёт два эквивалентных уравнения[21][23]
где — интеграл движения. Посредством вычитания этих уравнений и выражения в терминах декартовых координат импульса и можно показать, что эквивалентен вектору Лапласа — Рунге — Ленца
Этот подход Гамильтона — Якоби может использоваться, чтобы вывести сохраняющийся обобщённый вектор Лапласа — Рунге — Ленца в присутствии электрического поля [21][24]
где — заряд обращающейся частицы.
Альтернативная формулировка
В отличие от импульса и углового момента , у вектора Лапласа — Рунге — Ленца нет общепринятого определения. В научной литературе используются несколько различных множителей и символов. Самое общее определение даётся выше, но другое определение возникает после деления на постоянную , чтобы получить безразмерный сохраняющийся вектор эксцентриситета
где — вектор скорости. Направление этого масштабированного вектора совпадает с направлением , и его амплитуда равна эксцентриситету орбиты. Мы получим другие определения, если поделить на ,
или на
который имеет ту же размерность, что и угловой момент (вектор ). В редких случаях, знак вектора Лапласа — Рунге — Ленца может быть изменён на противоположный. Другие общие символы для вектора Лапласа — Рунге — Ленца включают , , , и . Однако выбор множителя и символа для вектора Лапласа — Рунге — Ленца, конечно же, не влияет на его сохранение.
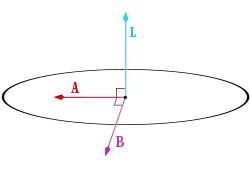
Альтернативный сохраняющийся вектор: бинормаль — вектор изучен Уильямом Гамильтоном[10]
который сохраняется и указывает вдоль малой полуоси эллипса. Вектор Лапласа — Рунге — Ленца является векторным произведением и (рис. 3). Вектор обозначен как бинормаль, так как он перпендикулярен как , так и . Подобно вектору Лапласа — Рунге — Ленца, вектор бинормали можно определить с различными множителями.
Два сохраняющиеся вектора, и можно объединить в сохраняющийся двухэлементный тензор
где обозначает тензорное произведение, а и — произвольные множители[11]. Записанное в компонентной записи, это уравнение читается так
Векторы и ортогональны друг другу, и их можно представить как главные оси сохраняющегося тензора , то есть как его собственные вектора. перпендикулярен
поскольку и перпендикулярны, то .
Вывод орбит Кеплера
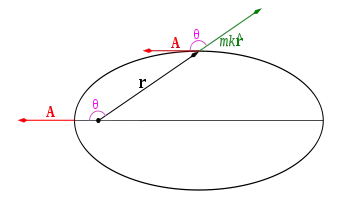
Форму и ориентацию орбиты в задаче Кеплера, зная вектор Лапласа — Рунге — Ленца , можно определить следующим образом. Рассмотрим скалярное произведение векторов и (положения планеты):
где является углом между и (рис. 4). Поменяем порядок множителей в смешанном произведении , и при помощи несложных преобразований получим определение для конического сечения:
с эксцентриситетом , заданным по формуле:
Приходим к выражению квадрата модуля вектора в виде
которое можно переписать, используя эксцентриситет орбиты
Таким образом, если энергия отрицательна, что соответствует связанным орбитам, эксцентриситет меньше, чем единица, и орбита имеет форму эллипса. Наоборот, если энергия положительна (несвязанные орбиты, также называемые орбитами рассеяния), эксцентриситет больше, чем единица, и орбита — гипербола. Наконец, если энергия точно равна нулю, эксцентриситет — единица, и орбита — парабола. Во всех случаях вектор направлен вдоль оси симметрии конического сечения и указывает на точку самого близкого положения точечной частицы от начала координат (перицентр).
Сохранение под действием силы, обратно пропорциональной квадрату расстояния
Сила , действующая на частицу, предполагается центральной. Поэтому
для некоторой функции радиуса . Поскольку угловой момент сохраняется под действием центральных сил, то и
где импульс записан в виде , и двойное векторное произведение упростилось с помощью формулы Лагранжа
Тождество
приводит к уравнению
Для специального случая центральной силы, зависящей обратно пропорциональной квадрату расстояния , последнее выражение равно
Тогда сохраняется в этом случае
Как показано ниже, вектор Лапласа — Рунге — Ленца является частным случаем обобщённого сохраняющегося вектора , который может быть определён для любой центральной силы[11][12]. Однако большинство центральных сил не формируют замкнутых орбит (см. теорема Бертрана), аналогичный вектор редко имеет простое определение и в общем случае представляет собой многозначную функцию угла между и .
Изменение под действием возмущающих центральных сил
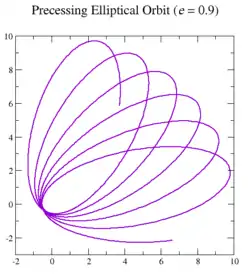
Во многих практических проблемах, типа планетарного движения, взаимодействие между двумя телами только приблизительно зависит обратно пропорционально квадрату расстояния. В таких случаях вектор Лапласа — Рунге — Ленца не постоянен. Однако, если возмущающий потенциал зависит только от расстояния, то полная энергия и вектор углового момента сохраняются. Поэтому траектория движения всё ещё находится в перпендикулярной к плоскости, и величина сохраняется, согласно уравнению . Следовательно, направление медленно вращается по орбите в плоскости. Используя каноническую теорию возмущений и координаты действие-угол, можно прямо показать[2], что вращается со скоростью
где — период орбитального движения и равенство использовалось, чтобы преобразовать интеграл по времени в интеграл по углу (рис. 5). Например, принимая во внимание эффекты общей теории относительности, приходим к добавке, которая в отличие от обычной гравитационной силы Ньютона зависит обратно пропорционально кубу расстояния[25]:
Подставляя эту функцию в интеграл и используя уравнение
чтобы выразить в терминах , скорость прецессии перицентра, вызванная этим возмущением, запишется в виде[25]
которая близка по значению к величине прецессии для Меркурия необъяснённой ньютоновской теорией гравитации[26]. Это выражение используется для оценки прецессии, связанной с поправками общей теории относительности для двойных пульсаров[27]. Это согласие с экспериментом является сильным аргументом в пользу общей теории относительности[28].
Теория групп
Теорема Нётер
Теорема Нётер утверждает, что инфинитезимальная вариация обобщённых координат физической системы
вызывает изменение функции Лагранжа в первом порядке на величину полной производной по времени
что соответствует сохранению величины
Эта компонента вектора Лапласа — Рунге — Ленца соответствует вариации координат[29]
где равняется 1, 2 и 3, а и — -е компоненты векторов положения и скорости , соответственно. Функция Лагранжа данной системы
Получающееся изменение в первом порядке малости для функции Лагранжа запишется как
Это приводит к сохранению компоненты
Преобразование Ли

Существует другой метод вывода сохранения вектора Лапласа — Рунге — Ленца, использующий вариацию координат без привлечения скоростей[30]. Масштабирование координат и времени с разной степенью параметра (рис. 6)
изменяет полный угловой момент и энергию :
— но сохраняет произведение . Отсюда следует, что эксцентриситет и величина сохраняются в уже упомянутом ранее уравнении
Направление также сохраняется, поскольку полуоси не изменяются при скалировании. Это преобразование оставляет верным третий закон Кеплера, а именно то, что полуось и период формируют константу .
Скобки Пуассона
Для трёх компонент вектора углового момента можно определить скобки Пуассона
где индекс пробегает значения 1, 2, 3 и — абсолютно антисимметричный тензор, то есть символ Леви-Чивита (третий индекс суммирования , чтобы не путать с силовым параметром , определённым выше). В качестве скобок Пуассона используются квадратные скобки (а не фигурные), как и в литературе и, в том числе, чтобы интерпретировать их как квантовомеханические коммутационные соотношения в следующем разделе.
Как показано выше, изменённый вектор Лапласа — Рунге — Ленца можно определить с той же размерностью, что и угловой момент, разделив на . Скобка Пуассона с вектором углового момента запишется в похожем виде
Скобка Пуассона с зависит от знака , то есть когда полная энергия отрицательна (эллиптические орбиты под действием центральной силы, зависящей обратно пропорционально квадрату расстояния) или положительная (гиперболические орбиты). Для отрицательных энергий скобки Пуассона примут вид
В то время как для положительных энергий скобки Пуассона имеют противоположный знак
Инварианты Казимира для отрицательных энергий определяются посредством следующих соотношений
и мы имеем нулевые скобки Пуассона для всех компонент и
равен нулю, из-за ортогональности векторов. Однако другой инвариант нетривиален и зависит только от , и . Этот инвариант можно использовать для вывода спектра атома водорода, используя только квантовомеханическое каноническое коммутационное соотношение, вместо более сложного уравнения Шрёдингера.
Законы сохранения и симметрия
Вариация координаты приводит к сохранению длины вектора Лапласа — Рунге — Ленца (см. теорема Нётер). Это сохранение можно рассматривать как некоторую симметрию системы. В классической механике, симметрии — непрерывные операции, которые отображают одну орбиту на другую, не изменяя энергию системы; в квантовой механике, симметрии — непрерывные операции, которые смешивают атомные орбитали, не изменяя полную энергию. Например, любая центральная сила приводя к сохранению углового момента . В физике обычно встречаются консервативные центральные силы, обладающие симметрией группы вращения SO(3). Классически, полное вращение системы не затрагивает энергию орбиты; квантовомеханически, вращения смешивают сферические функции с тем же самым квантовым числом (вырожденные состояния), не изменяя энергию.
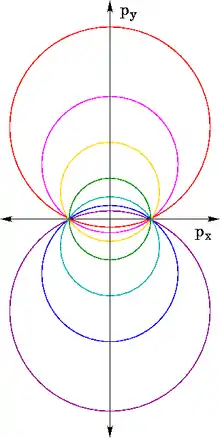
Симметрия повышается для центральной силы, обратной квадрату расстояния. Специфическая симметрия проблемы Кеплера приводит к сохранению как вектора углового момента , так и вектора Лапласа — Рунге — Ленца (как определено выше) и квантовомеханически гарантирует, что уровни энергии атома водорода не зависят от квантовых чисел углового момента и . Симметрия является более тонкой, потому что операция симметрии должна иметь место в пространстве большей размерности; такие симметрии часто называют скрытыми симметриями[30]. Классически, более высокая симметрия проблемы Кеплера учитывает непрерывные изменения орбит, которые сохраняют энергию, но не угловой момент; другими словами, орбиты с одинаковой энергией, но различными угловыми моментами (эксцентриситетом) могут быть преобразованы непрерывно друг в друга. Квантовомеханически это соответствует смешиванию орбиталей, которые отличаются квантовыми числами и , атомные орбитали типа () и (). Такое смешивание нельзя произвести с обычными трёхмерными трансляциями или вращениями, но оно эквивалентно вращению в пространстве с более высоким измерением.
Связанная система с отрицательной полной энергией обладает симметрией SO(4), которая сохраняет длину четырёхмерных векторов
В 1935 году Владимир Фок показал, что квантовомеханическая проблема Кеплера эквивалентна проблеме свободной частицы, ограниченной четырёхмерной гиперсферой[7]. В частности, Фок показал, что волновая функция уравнения Шрёдингера в пространстве импульсов для проблемы Кеплера представляет собой четырёхмерное обобщение стереографической проекции сферических функций из 3-сферы в трёхмерное пространство. Вращение гиперсферы и перепроектирование приводит к непрерывному преобразованию эллиптических орбит, не изменяющему энергию; квантовомеханически это соответствует смешиванию всех орбиталей с одинаковым главным квантовым числом . Валентин Баргман отметил впоследствии, что скобки Пуассона для вектора углового момента и скалированного вектора Лапласа — Рунге — Ленца формируют алгебру Ли для .[8] Проще говоря, эти шесть величин и соответствуют шести сохраняющимся угловым импульсам в четырёх измерениях, связанных с шестью возможными простыми вращениями в этом пространстве (есть шесть способов выбрать две оси из четырёх). Это заключение не подразумевает, что наша Вселенная — четырёхмерная гиперсфера; это просто означает, что эта специфическая проблема физики (проблема двух тел для центральной силы, зависящей обратно квадрату расстояния) математически эквивалентна свободной частице на четырёхмерной гиперсфере.
Рассеянная система с положительной полной энергией обладает симметрией SO(3,1), которая сохраняет длину 4-вектора в пространстве с метрикой Минковского
Фок[7] и Баргман[8] рассмотрели как отрицательные, так и положительные энергии. Они также были рассмотрены энциклопедически Бендером и Ициксоном[31][32]. Недавнее исследование Ефимова С.П. показало, что результат В. Фока переносится из искривленного импульсного пространства в 4-х мерное координатное [33]. При этом переход от четырехмерных сферических функций в физическое трехмерное пространство возникает просто при замене четвертой "лишней" координаты на мнимый радиус вектор . Найденное координатное пространство оказывается в теории "ближе", чем искривленное пространство В. Фока.
Симметрия вращений в четырёхмерном пространстве

Связь между проблемой Кеплера и вращениями в четырёхмерном пространстве SO(4) можно достаточно просто визуализировать[31][34][35]. Пусть в четырёхмерном пространстве заданы декартовы координаты, которые обозначены , где представляют декартовы координаты обычного положения трёхмерного вектора . Трёхмерный вектор импульса связан с четырёхмерным вектором на четырёхмерной единичной сфере посредством
где — единичный вектор вдоль новой оси . Поскольку имеет только три независимые компоненты, то этот вектор можно обратить, получив выражение для . Например, для компоненты
и аналогично для и . Другими словами, трёхмерный вектор является стереографической проекцией четырёхмерного вектора , умноженному на (рис. 8).
Без потери общности, мы можем устранить нормальную вращательную симметрию, выбирая декартовы координаты, где ось направлена вдоль вектора углового момента , и годограф импульса расположен как показано на рисунке 7, с центрами кругов на оси . Так как движение происходит в плоскости, а и ортогональны, , и внимание можно сосредоточить на трёхмерном векторе . Семейство окружностей Аполлония годографов импульса (рис. 7) соответствует множеству больших кругов на трёхмерной сфере , все из которых пересекают ось в этих двух фокусах , соответствующих фокусам годографа импульса при . Большие круги связаны простым вращением вокруг оси (рис. 8). Эта вращательная симметрия преобразует все орбиты с той же самой энергией друг в друга; однако, такое вращение ортогонально к обычным трёхмерным вращениям, так как оно преобразует четвёртое измерение . Эта более высокая симметрия характерна для проблемы Кеплера и соответствует сохранению вектора Лапласа — Рунге — Ленца.
Изящное решение для проблемы Кеплера с использованием переменных угол-действие можно получить, избавляясь от избыточной четырёхмерной координаты и используя эллиптические цилиндрические координаты [36]
где используются эллиптические функции Якоби: , и .
Применение и обобщения
Квантовая механика атома водорода
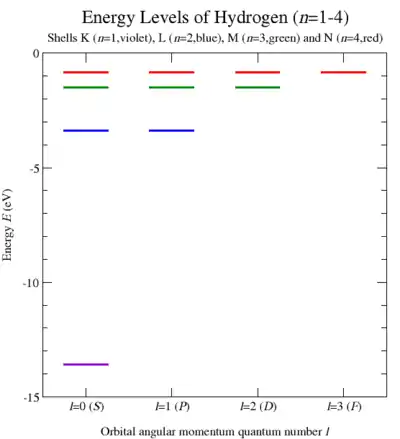
Скобки Пуассона дают простой способ для квантования классической системы. Коммутатор двух квантовомеханических операторов равняется скобке Пуассона соответствующих классических переменных, умноженной на [37]. Выполняя это квантование и вычисляя собственные значения оператора Казимира для проблемы Кеплера, Вольфганг Паули вывел энергетический спектр водородоподобного атома (рис. 9) и, таким образом, его атомный эмиссионный спектр[3]. Это изящное решение было получено до получения уравнения Шрёдингера[38].
Особенность квантовомеханического оператора для вектора Лапласа — Рунге — Ленца заключается в том, что импульс и операторы углового момента не коммутируют друг с другом, следовательно, векторное произведение и должно быть определено тщательно[39]. Как правило, операторы в декартовой системе координат определены с помощью симметризованного произведения
из которого определяются соответствующие лестничные операторы
Нормированный оператор первого инварианта Казимира может быть определён подобным образом
где — оператор, обратный к оператору энергии (гамильтониан) и — единичный оператор. Применяя эти лестничные операторы к собственным состояниям операторов полного углового момента, азимутального углового момента и энергии, можно показать, что собственные состояния первого оператора Казимира задаются формулой . Следовательно, уровни энергии даются выражением
которое идентично формуле Ридберга для атома водорода (рис 9).
Обобщение на другие потенциалы и СТО
Вектор Лапласа — Рунге — Ленца был обобщён на другие потенциалы и даже на специальную теорию относительности. Наиболее общую форму этого вектора можно записать в виде[11]
где (см. теорема Бертрана) и , с углом , определённым как
Здесь — релятивистский фактор. Как и раньше, можно получить сохраняющийся вектор бинормали , взяв векторное произведение с сохраняющимся вектором углового момента
Эти два вектора можно соединить в сохраняющийся двухкомпонентный тензор
Для примера вычислим вектор Лапласа — Рунге — Ленца для нерелятивистского изотропного гармонического осциллятора.[11] Рассмотрим центральную силу:
вектор углового момента сохраняется, и поэтому движение происходит в плоскости. Сохраняющийся тензор можно переписать в более простом виде:
хотя нужно заметить, что и не перпендикулярны, как и . Соответствующий вектор Лапласа — Рунге — Ленца имеет более сложную запись
где — частота осциллятора.
Литература
- Арнольд В. И. . Математические методы классической механики. 5-е изд. — М.: Едиториал УРСС, 2003. — 416 с. — ISBN 5-354-00341-5.; в сети в электронном виде есть 3-е изд. за 1988 год, см. Добавление 8, на стр. 381
- Голдстейн Г. . Классическая механика. 2-е изд. — М.: Наука, 1975. — 415 с.
- Pauli, W. Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik (нем.) // Zeitschrift für Physik : magazin. — 1926. — Bd. 36. — S. 336—363.
- Hamilton, W. R. The Hodograph, or a new Method of expressing in symbolical Language the Newtonian Law of Attraction (англ.) // Proceedings of the Royal Irish Academy : journal. — 1847. — Vol. 3. — P. 344—353.
- Хикок Ф. А. . Графики космического полёта. — М.: Машиностроение, 1968. — 133 с. — Гл. 3. Анализ траекторий с помощью полярных диаграмм, с. 42.
- Гулд Х., Тобочник Я. . Компьютерное моделирование в физике. Т. 1. — М.: Мир, 1990. — 352 с. — ISBN 5-03-001593-0.. — Задача 4.9. Свойства орбит в пространстве скоростей, с. 88.
- Fock, V. Zur Theorie des Wasserstoffatoms (нем.) // Zeitschrift für Physik : magazin. — 1935. — Bd. 98. — S. 145—154.
- Bargmann, V. Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock (нем.) // Zeitschrift für Physik : magazin. — 1936. — Bd. 99. — S. 576—582.
- Goldstein, H. Prehistory of the Runge-Lenz vector (англ.) // American Journal of Physics : journal. — 1975. — Vol. 43. — P. 735—738.
Goldstein, H. More on the prehistory of the Runge-Lenz vector (англ.) // American Journal of Physics : journal. — 1976. — Vol. 44. — P. 1123—1124. - Hamilton, W. R. On the Application of the Method of Quaternions to some Dynamical Questions (англ.) // Proceedings of the Royal Irish Academy : journal. — 1847. — Vol. 3. — P. Appendix III, pp. xxxvi—l.
- Fradkin, D. M. Existence of the Dynamic Symmetries O4 and SU3 for All Classical Central Potential Problems (англ.) // Progress of Theoretical Physics : journal. — 1967. — Vol. 37. — P. 798—812.
- Yoshida, T. Two methods of generalisation of the Laplace-Runge-Lenz vector (англ.) // European Journal of Physics : journal. — 1987. — Vol. 8. — P. 258—259.
- Hermann, J. Metodo d'investigare l'orbite de' pianeti // Giornale de Letterati D'Italia. — 1710. — Т. 2. — С. 447—467.
Hermann, J. Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710 (фр.) // Histoire de l'academie royale des sciences (Paris) : magazine. — 1710. — Vol. 1732. — P. 519—521. - Bernoulli, J. Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710 (фр.) // Histoire de l'academie royale des sciences (Paris) : magazine. — 1710. — Vol. 1732. — P. 521—544.
- Laplace P. S. . Traité de mécanique celeste. Tome I, Premiere Partie, Livre II. — Paris, 1799. — P. 165ff.
- Gibbs J. W., Gibbs E. B. . Vector Analysis. — New York: Scribners, 1901. — 436 p. — P. 135.
- Runge C. . Vektoranalysis. Bd. I. — Leipzig: Hirzel, 1919. — 436 p.
- Lenz, W. Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung (нем.) // Zeitschrift für Physik : magazin. — 1924. — Bd. 24. — S. 197—207.
- Evans, N. W. Superintegrability in classical mechanics (англ.) // Physical Review A : journal. — 1990. — Vol. 41. — P. 5666—5676.
- Зоммерфельд А. . Atomic Structure and Spectral Lines. — London: Methuen, 1923. — 118 p.
- Landau L. D., Lifshitz E. M. . Mechanics. 3rd ed. — Pergamon Press, 1976. — ISBN 0-08-029141-4.. — P. 154; Ландау Л. Д., Лифшиц Е. М. . Механика. 5-е изд. — М.: Физматлит, 2004. — 224 с. — (Курс теоретической физики, том 1). — ISBN 5-9221-0055-6. — § 15. Кеплерова задача, «сохраняющийся вектор», с. 56; § 52. Условно-периодическое движение, задача с решением в полярных координатах, с. 217.
- Evans, N. W. Group theory of the Smorodinsky-Winternitz system (англ.) // Journal of Mathematical Physics : journal. — 1991. — Vol. 32. — P. 3369—3375.
- Dulock, V. A.; McIntosh H. V. On the Degeneracy of the Kepler Problem (англ.) // Pacific Journal of Mathematics : journal. — 1966. — Vol. 19. — P. 39—55.
- Redmond, P. J. Generalization of the Runge-Lenz Vector in the Presence of an Electric Field (англ.) // Physical Review : journal. — 1964. — Vol. 133. — P. B1352—B1353.
- Einstein, A. Erklärung der Perihelbeivegung der Merkur aus der allgemeinen Relativitätstheorie (нем.) // Sitzungsberichte der der Königlich Preußischen Akademie der Wissenschaften : magazin. — 1915. — Bd. 47, Nr. 2. — S. 831—839.
- Le Verrier, U. J. J. Sur la théorie de Mercure et sur le mouvement du périhélie de cette planète; Lettre de M. Le Verrier à M. Faye (фр.) // Comptes Rendus de l'Academie de Sciences (Paris) : magazine. — 1859. — Vol. 49. — P. 379—383.
- Will C. M. . General Relativity, an Einstein Century Survey / Ed. by S. W. Hawking and W. Israel. — Cambridge: Cambridge University Press, 1979.
- Pais, A. Subtle is the Lord: The Science and the Life of Albert Einstein (англ.). — Oxford University Press, 1982.
Пайс, Абрахам. . Научная деятельность и жизнь Альберта Эйнштейна / Под ред. А. А. Логунова. — М.: Наука, 1989. — 566 с. — ISBN 5-02-014028-7.. - Lévy-Leblond, J. M. (1971). “Conservation Laws for Gauge-Invariant Lagrangians in Classical Mechanics”. American Journal of Physics. 39 (5): 502—506. Bibcode:1971AmJPh..39..502L. DOI:10.1119/1.1986202.
- Prince, G. E.; Eliezer C. J. On the Lie symmetries of the classical Kepler problem (англ.) // Journal of Physics A: Mathematical and General : journal. — 1981. — Vol. 14. — P. 587—596.
- Bander, M.; Itzykson C. Group Theory and the Hydrogen Atom (I) (англ.) // Reviews of Modern Physics : journal. — 1966. — Vol. 38. — P. 330—345.
- Bander, M.; Itzykson C. Group Theory and the Hydrogen Atom (II) (англ.) // Reviews of Modern Physics : journal. — 1966. — Vol. 38. — P. 346—358.
- Ефимов С.П. Трансформация теории Фока в координатное пространство. Гармонические тензоры в квантовой задаче Кулона (рус.) // УФН : journal. — 2022. — Т. 192. — doi:10.3367/UFNr.2021.04.038966.
- Rogers, H. H. Symmetry transformations of the classical Kepler problem (англ.) // Journal of Mathematical Physics : journal. — 1973. — Vol. 14. — P. 1125—1129.
- Guillemin, V.; Sternberg S. Variations on a Theme by Kepler. — American Mathematical Society Colloquium Publications, volume 42, 1990..
- Lakshmanan, M.; Hasegawa H. On the canonical equivalence of the Kepler problem in coordinate and momentum spaces (англ.) // Journal of Physics A : journal. — Vol. 17. — P. L889—L893.
- Dirac P. A. M. . Principles of Quantum Mechanics. 4th edition (англ.). — Oxford University Press, 1958.
- Schrödinger, E. Quantisierung als Eigenwertproblem // Annalen der Physik. — 1926. — Т. 384. — С. 361—376.
- Bohm A. . Quantum Mechanics: Foundations and Applications. 2nd edition. — Springer Verlag, 1986. — P. 208—222.
Ссылки
- Leach, P.G.L.; G.P. Flessas. Generalisations of the Laplace — Runge — Lenz vector (англ.) // J. Nonlinear Math. Phys. : journal. — 2003. — Vol. 10. — P. 340—423. Статья посвящена обобщению вектора Лапласа — Рунге — Ленца на потенциалы, отличные от кулоновского. arxiv.org