Формула Ридберга
Фо́рмула Ри́дберга — эмпирическая формула, описывающая длины волн в спектрах излучения атомов химических элементов. Предложена шведским учёным Йоханнесом Ридбергом и представлена 5 ноября 1888 года.
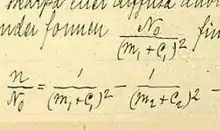
Формула Ридберга для водородоподобных атомов выглядит следующим образом:
- где — длина волны света в вакууме;
- — постоянная Ридберга в общем случае различна для разных химических элементов;
- — атомный номер, или число протонов в ядре атома данного элемента;
- и — целые числа, такие что .
История
В 1880-х годах, Ридберг работал над формулой, описывающей взаимосвязь между длинами волн в спектрах щелочных металлов. Он заметил, что линии образуют серии, и обнаружил, что может уменьшить трудоёмкость расчётов, введя спектроскопическое волновое число (величина, равная обратная длине волны, обозначается как ) в качестве единицы измерения. Он записал волновые числа () следующих друг за другом линий в каждой серии напротив расположенных параллельно в соответствующем порядке целых чисел, представляющих собой порядок линии в данной конкретной серии. Обнаружив, что получившиеся кривые имели похожие формы, он нашёл единую функцию, описывающую все эти кривые, при подстановке в неё соответствующих констант.
Сначала он проверил формулу где — волновое число спектральной линии, — граница серии, — порядковый номер линии в серии (константа, различная для разных серий) и — универсальная константа. Эта формула не давала достаточно точных результатов.
Затем Ридберг проверил формулу когда ему стала известна формула Бальмера для спектра атома водорода В этой формуле,
Ридберг переписал формулу Бальмера, используя обозначения волновых чисел, в следующем виде:
Это преобразование подсказало, что формула Бальмера для водорода может являться частным случаем при и где — обратно константе Бальмера.
Величина как было установлено позже, была универсальной константой, общей для всех элементов, равной Эта константа сейчас называют постоянной Ридберга, и величину называют квантовый дефект.
Как подчеркнул Нильс Бор[1], выражение результатов через волновые числа, а не через длины волн, было ключом к открытию Ридберга. Фундаментальная роль волновых чисел была особо подчёркнута открытием комбинационного принципа Ридберга — Ритца в 1908 году. Фундаментальная причина важности волновых чисел лежит в области квантовой механики, так как энергия фотонов с разной длиной волны прямо пропорциональна волновым числам.
Волновые числа световых волн пропорциональны частоте и поэтому также пропорциональны энергии квантов света То есть, Современное понимание состоит в том, что графики Ридберга были упрощёнными (обладали невысокой степенью адекватности реальным зависимостям), так как отражали лишь простые свойства в поведении спектральных линий в условиях строго определённых (квантованных) разностей энергий между электронными орбиталями в атоме.
Классическое выражение Ридберга (в работе 1888 года) для длин волн спектральных серий не имело физическое объяснение. Пред-квантовое объяснение Ритца (1908 год) механизма «образования» спектральных серий состояло в том, что электроны в атоме ведут себя как постоянные магниты, и что эти магниты могут колебаться относительно атомного ядра (по крайней мере в течение некоторого времени), порождая электромагнитное излучение[2]. Это явление впервые было понято Нильсом Бором в 1913 году так, как оно включено в описание Боровская модель атома.
В боровской модели атома целые числа Ридберга (и Бальмера) соответствуют электронным орбиталям на различных определённых расстояниях от ядра атома. Частота (или энергия), получается при переходе с уровня на уровень поэтому представляет собой энергию фотона, излучённого или поглощённого, когда электрон «перепрыгивает» с орбитали (уровня) 1 на орбиталь 2.
Формула Ридберга для атома водорода
- где — длина волны электромагнитного излучения в вакууме;
- — постоянная Ридберга;
- и — целые числа, причём
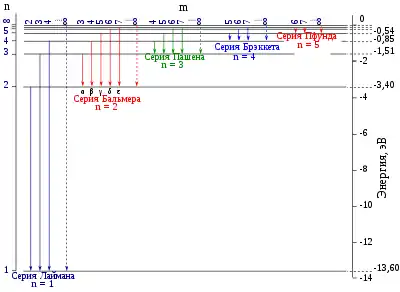
Принимая равным 1, и полагая, что может принимать целые значения от 2 до бесконечности, получаем спектральные линии, известные как серия Лаймана, коротковолновая граница длин волн которых стремится к 91 нм. При подстановке в формулу равным 2, 3, и т. д. аналогично получаются и другие спектральные серии:
| n | m | Название серии | Коротковолновая граница серии |
|---|---|---|---|
| 1 | 2 → ∞ | Серия Лаймана | 91,13 нм (Ультрафиолетовая часть спектра) |
| 2 | 3 → ∞ | Серия Бальмера | 364,51 нм (Видимая часть спектра) |
| 3 | 4 → ∞ | Серия Пашена | 820,14 нм (Инфракрасная часть спектра) |
| 4 | 5 → ∞ | Серия Брэккета | 1458,03 нм (Инфракрасная часть спектра) |
| 5 | 6 → ∞ | Серия Пфунда | 2278,17 нм (Инфракрасная часть спектра) |
| 6 | 7 → ∞ | Серия Хэмпфри | 3280,56 нм (Инфракрасная часть спектра) |
Формула Ридберга для любых водородоподобных атомов
Формула для атома водорода, приведённая выше, может быть дополнена для применения к любым водородоподобным атомам:
- где — длина волны света в вакуум;
- — постоянная Ридберга для данного химического элемента;
- — порядковый номер элемента в периодической таблице, то есть, количество протонов в атомных ядрах данного элемента;
- и — целые числа, причём
Важно заметить, что эта формула применима только для водородоподобных атомов, то есть для таких атомов, которые содержат в электронной оболочке только один электрон. Такими атомами являются, например, и любые другие многократно ионизированные атомы с одним электроном в электронной оболочке.
Формула Ридберга позволяет получать правильные значения длин волн для атомов, находящихся в высоких степенях возбуждения, когда эффективный заряд ядра можно считать таким же как и у водорода, когда все, кроме одного, заряды в ядре экранированы другими электронами, и центр атома имеет эффективный положительный заряд, равный +1.
Для других спектральных переходов в многоэлектронных атомах, формула Ридберга даёт некорректные результаты, поскольку величина экранирования внутренних электронов для переходов внешних электронов варьируется, и нет возможности сделать в формуле подобную простую «компенсирующую» «ослабление действия заряда ядра» поправку, как приведено выше.
Формула Ридберга для характеристического рентгеновского излучения
При определённом изменении (замене на и использовании целых чисел дающих численное значение для разности их обратных квадратов (в формуле выше)), формула Ридберга даёт корректные результаты в специальном случае K-альфа линий, подобные переходы являются K-альфа переходом электрона с орбитали на орбиталь называемом характеристическим рентгеновским излучением. Это аналогично переходу, соответствующего линии Лаймана-альфа, для водорода, и имеет тот же самый частотный множитель. Поскольку 2p-электрон не экранирован от ядра в атоме никакими другими электронами, то заряд ядра ослаблен единственным остающимся 1s-электроном, делая атом быть фактически водородоподобным атомом, но со сниженным зарядом ядра Частота излучения для этого перехода, таким образом, является частотой линии Лайман-альфа атома водорода, возрастая, благодаря величине Эта формула исторически известна как закон Мозли (добавляя скорость света в формулу для замены длины волны на частоту), и может быть использована для вычисления длин волн (K-альфа) рентгеновских спектральных линий в рентгеновских спектрах излучения химических элементов от алюминия до золота. Об исторической важности этого закона можно узнать, ознакомившись с биографией Генри Мозли. Этот закон был эмпирически установлен примерно в то же время, когда была создана боровская модель атома.
Примечания
- Bohr, N. Rydberg's discovery of the spectral laws // Collected works / Kalckar, J.. — Amsterdam: North-Holland Publ. Cy., 1985. — Т. 10. — С. 373—379.
- Ritz, W. Magnetische Atomfelder und Serienspektren (нем.) // Annalen der Physik : magazin. — 1908. — Bd. 330, Nr. 4. — S. 660—696. — doi:10.1002/andp.19083300403.
Ссылки
- Sutton, Mike. Getting the numbers right: The lonely struggle of the 19th century physicist/chemist Johannes Rydberg (англ.) // Chemistry World : magazine. — 2004. — July (vol. 1, no. 7). — P. 38—41. — ISSN 1473-7604.
- Martinson, I.; Curtis, L.J. Janne Rydberg – his life and work (англ.) // Nuclear Instruments and Methods in Physics Research Section B. — 2005. — Vol. 235, no. 1—4. — P. 17—22. — doi:10.1016/j.nimb.2005.03.137. — .
