Консервативные силы

В физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.

В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной (см. Фундаментальные взаимодействия). В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.

Некоторые авторы консервативными силами считают механические силы, работа которых по любой замкнутой траектории равна нулю и зависящие только от координат[2][3]. Если механические силы зависят не только от координат, но и скоростей и направлены всегда перпендикулярно скорости, то они называются гироскопическими силами[4][5].

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

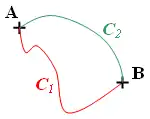
Для консервативных сил выполняются следующие равенства:

${\displaystyle \int \limits _{C_{1}}{\vec {F}}\cdot d{\vec {l}}=\int \limits _{C_{2}}{\vec {F}}\cdot d{\vec {l}}}$ — работа, производимая консервативной силой, определяется только начальным и конечным положениями точки её приложения и не зависит от выбора траектории, по которой перемещается тело;

${\displaystyle \oint \limits _{C}{{\vec {F}}\cdot d{\vec {l}}}=0}$ — работа консервативных сил по произвольному замкнутому контуру равна 0;

${\displaystyle \nabla \times {\vec {F}}=0}$ — ротор консервативных сил равен 0;

${\displaystyle {\vec {F}}=\nabla U}$ — консервативная сила является градиентом некой скалярной функции ${\displaystyle U}$, называемой силовой. Эта функция равна потенциальной энергии ${\displaystyle E_{p},}$ взятой с обратным знаком. Соответственно, ${\displaystyle {\vec {F}}}$ и ${\displaystyle E_{p}}$ связаны соотношением

${\displaystyle {\vec {F}}=-\nabla E_{p}.}$

Таким образом, консервативная сила всегда направлена в сторону уменьшения потенциальной энергии.